题目内容
根据下列条件,分别求出对应的二次函数关系式.
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
解:(1)∵抛物线顶点(-1,-2),
∴设所求二次函数关系式为y=a(x+1)2-2,
把(1,10)代入上式,得10=a(1+1)2-2.
∴a=3,
∴所求二次函数关系式为y=3(x+1)2-2,即y=3x2+6x+1.
(2)设所求二次函数关系为y=ax2+bx+c,
把(0,-2),(1,0),(2,3)分别代入y=ax2+bx+c,
得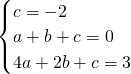 ,
,
解得: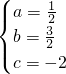
∴此抛物线的函数解析式为:y=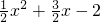 .
.
分析:(1)由抛物线顶点坐标设出函数关系式为y=a(x+1)2-2,再把(1,10)代入求得a即可.
(2)设所求函数关系式为y=ax2+bx+c,再把(0,-2),(1,0),(2,3)代入求得a,b,c即可.
点评:本题考查了二次函数关系式的求法,需注意题中给出的条件不同,则二次函数关系式的设法不同.
∴设所求二次函数关系式为y=a(x+1)2-2,
把(1,10)代入上式,得10=a(1+1)2-2.
∴a=3,
∴所求二次函数关系式为y=3(x+1)2-2,即y=3x2+6x+1.
(2)设所求二次函数关系为y=ax2+bx+c,
把(0,-2),(1,0),(2,3)分别代入y=ax2+bx+c,
得
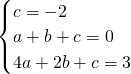 ,
,解得:
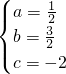
∴此抛物线的函数解析式为:y=
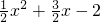 .
.分析:(1)由抛物线顶点坐标设出函数关系式为y=a(x+1)2-2,再把(1,10)代入求得a即可.
(2)设所求函数关系式为y=ax2+bx+c,再把(0,-2),(1,0),(2,3)代入求得a,b,c即可.
点评:本题考查了二次函数关系式的求法,需注意题中给出的条件不同,则二次函数关系式的设法不同.

练习册系列答案
相关题目