题目内容
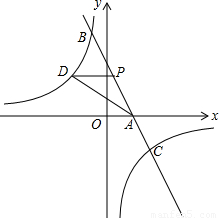
如图,已知一次函数y1=kx+b图象与x轴相交于点A,与反比例函数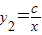 的图象相交于B(-1,5)、C(
的图象相交于B(-1,5)、C( ,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.
,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.(1)求k、b的值;
(2)设-1<m<
 ,过点P作x轴的平行线与函数
,过点P作x轴的平行线与函数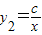 的图象相交于点D.试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;
的图象相交于点D.试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;(3)设m=1-a,如果在两个实数m与n之间(不包括m和n)有且只有一个整数,求实数a的取值范围.
【答案】分析:(1)B、C两点在反比例函数图象上,根据反比例函数图象上点的横纵坐标的积相等,可求d的值,将B、C两点坐标代入y1=kx+b中,列方程组可求k、b的值;
(2)存在,根据直线解析式可求A点坐标,点P在直线上,点P( ,n),PD∥x轴,则D、P的纵坐标都是n,此时,D(-
,n),PD∥x轴,则D、P的纵坐标都是n,此时,D(- ,n),则PD=
,n),则PD=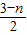 +
+ ,由S=
,由S= •n•PD,可求△PAD的面积表达式,利用二次函数的性质求最大值;
•n•PD,可求△PAD的面积表达式,利用二次函数的性质求最大值;
(3)点P(m,n)在一次函数图象上,由一次函数解析式可知,设m=1-a,则P(1-a,2a+1),依题意m≠n,可知a≠0,根据a>0和a<0两种情况,分别求实数a的取值范围.
解答:解:(1)将B点的坐标代入y2= ,得c=-5,
,得c=-5,
则y2=- ,
,
把x= 代入得y=-2,
代入得y=-2,
则C( ,-2)
,-2)
将B、C代入直线y1=kx+b得: ;
;
(2)存在.
令y1=0,x= ,则A的坐标是:(
,则A的坐标是:( ,0);
,0);
由题意,点P在线段AB上运动(不含A,B),
设点P(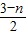 ,n),
,n),
∵DP平行于x轴,
∴D、P的纵坐标都是n,
∴D的坐标是:(- ,n),
,n),
∴S= •n•PD=
•n•PD= (
( +
+ )×n=-
)×n=- (n-
(n- )2+
)2+ ;
;
而-2m+3=n,得0<n<5;
所以由S关于n的函数解析式,所对应的抛物线开口方向决定,当n= ,即P(
,即P( ,
, ),S的最大值是:
),S的最大值是: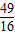 .
.
(3)由已知P(1-a,2a+1),易知,m≠n,1-a≠2a+1,a≠0;
若a>0,m<1<n,由题设m≥0,n≤2,
则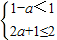 ,
,
解不等式组的解集是:0<a≤ ;
;
若a<0,n<1<m,由题设n≥0,m≤2,
则 ,
,
解得:- ≤a<0;
≤a<0;
综上:a的取值范围是:- ≤a<0,0<a≤
≤a<0,0<a≤ .
.
点评:本题考查了反比例函数的综合运用.关键是根据反比例函数图象上点的横纵坐标积相等求C点坐标,由“两点法”求直线解析式,根据平行于x轴直线上点的坐标特点,表示三角形的面积,根据二次函数的性质求最大值,本题还考查了分类讨论的思想.
(2)存在,根据直线解析式可求A点坐标,点P在直线上,点P(
 ,n),PD∥x轴,则D、P的纵坐标都是n,此时,D(-
,n),PD∥x轴,则D、P的纵坐标都是n,此时,D(- ,n),则PD=
,n),则PD=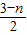 +
+ ,由S=
,由S= •n•PD,可求△PAD的面积表达式,利用二次函数的性质求最大值;
•n•PD,可求△PAD的面积表达式,利用二次函数的性质求最大值;(3)点P(m,n)在一次函数图象上,由一次函数解析式可知,设m=1-a,则P(1-a,2a+1),依题意m≠n,可知a≠0,根据a>0和a<0两种情况,分别求实数a的取值范围.
解答:解:(1)将B点的坐标代入y2=
 ,得c=-5,
,得c=-5,则y2=-
 ,
,把x=
 代入得y=-2,
代入得y=-2,则C(
 ,-2)
,-2)将B、C代入直线y1=kx+b得:
 ;
;(2)存在.
令y1=0,x=
 ,则A的坐标是:(
,则A的坐标是:( ,0);
,0);由题意,点P在线段AB上运动(不含A,B),
设点P(
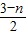 ,n),
,n),∵DP平行于x轴,
∴D、P的纵坐标都是n,
∴D的坐标是:(-
 ,n),
,n),∴S=
 •n•PD=
•n•PD= (
( +
+ )×n=-
)×n=- (n-
(n- )2+
)2+ ;
;而-2m+3=n,得0<n<5;
所以由S关于n的函数解析式,所对应的抛物线开口方向决定,当n=
 ,即P(
,即P( ,
, ),S的最大值是:
),S的最大值是: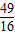 .
.(3)由已知P(1-a,2a+1),易知,m≠n,1-a≠2a+1,a≠0;
若a>0,m<1<n,由题设m≥0,n≤2,
则
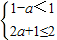 ,
,解不等式组的解集是:0<a≤
 ;
;若a<0,n<1<m,由题设n≥0,m≤2,
则
 ,
,解得:-
 ≤a<0;
≤a<0;综上:a的取值范围是:-
 ≤a<0,0<a≤
≤a<0,0<a≤ .
.点评:本题考查了反比例函数的综合运用.关键是根据反比例函数图象上点的横纵坐标积相等求C点坐标,由“两点法”求直线解析式,根据平行于x轴直线上点的坐标特点,表示三角形的面积,根据二次函数的性质求最大值,本题还考查了分类讨论的思想.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
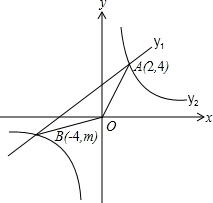 B(-4,m)两点.
B(-4,m)两点.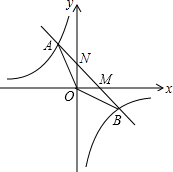 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数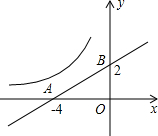 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数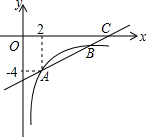 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数