题目内容
将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点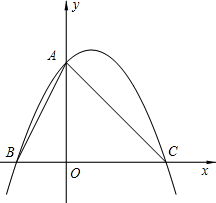 ,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).(1)求该抛物线的解析式;
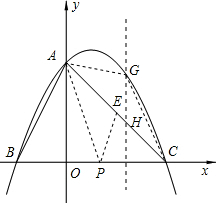
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,设点P的横坐标为x,试用含x的代数式表示△APE的面积S;
(3)在(2)的条件下,点G为第一象限内的该抛物线上的一个动点,对于S的一个确定的值,始终存在点G,满足△AGC的面积与(2)中△APE的面积相等,求符合题意的点G的横坐标的取值范围.
分析:(1)根据C(6,0),B(-3,0),运用交点式求出二次函数解析式;
(2)利用相似三角形的性质得出S△PCE=
,进而求出△APE的面积S;
(3)表示出S△AGC=
GH•CO=-x2+6x,进而求出x的取值范围.
(2)利用相似三角形的性质得出S△PCE=
| (x-6) 2 |
| 3 |
(3)表示出S△AGC=
| 1 |
| 2 |
解答:(1)由题意得,A(0,6),C(6,0),B(-3,0),
解:设抛物线解析式为:y=a(x+3)(x-6),
解得:a=-
,
∴y=-
(x+3)(x-6),
=-
x2+x+6,
(2)如图,∵PE∥AB,
∴△PCE∽△BCA,
∴
=
,
=
,
∴S△PCE=
,
∴S=S△APC-S△PCE=-
x2+x+6,
=-
(x-
)2+
,
(当x=
时,S有最大值为
);
故S的取值范围是:0<S≤
,(-3<x<6);
(3)设G(x,-
x2+x+6)
过G作GH∥y轴交直线AC于点H,
易得直线AC:y=-x+6,
∴H(x,-x+6)
∴GH=-
x2+x+6-(-x+6)=-
x2+2x,
∴S△AGC=
GH•CO=-x2+6x=-(x-3)2+9,
故S△AGC的取值范围是:0<S△AGC≤9,(0<x<6);
当S△AGC=
时,-x2+6x=
,
解得:x1=
,x2=
,
∴点G的横坐标x的取值范围是0<x≤
或
≤x<6时.
解:设抛物线解析式为:y=a(x+3)(x-6),
解得:a=-
| 1 |
| 3 |
∴y=-
| 1 |
| 3 |
=-
| 1 |
| 3 |
(2)如图,∵PE∥AB,
∴△PCE∽△BCA,
∴
| S△PCE |
| S△BCA |
| PC2 |
| BC2 |
| S△PCE |
| 27 |
| (6-x)2 |
| 81 |
∴S△PCE=
| (x-6) 2 |
| 3 |
∴S=S△APC-S△PCE=-
| 1 |
| 3 |
=-
| 1 |
| 3 |
| 3 |
| 2 |
| 27 |
| 4 |
(当x=
| 3 |
| 2 |
| 27 |
| 4 |

故S的取值范围是:0<S≤
| 27 |
| 4 |
(3)设G(x,-
| 1 |
| 3 |
过G作GH∥y轴交直线AC于点H,
易得直线AC:y=-x+6,
∴H(x,-x+6)
∴GH=-
| 1 |
| 3 |
| 1 |
| 3 |
∴S△AGC=
| 1 |
| 2 |
故S△AGC的取值范围是:0<S△AGC≤9,(0<x<6);
当S△AGC=
| 27 |
| 4 |
| 27 |
| 4 |
解得:x1=
| 3 |
| 2 |
| 9 |
| 2 |
∴点G的横坐标x的取值范围是0<x≤
| 3 |
| 2 |
| 9 |
| 2 |
点评:此题主要考查了二次函数的综合题目,利用交点式求二次函数解析式以及相似三角形的性质是考查的重点内容,同学们应学会应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
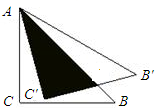 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.| A、12.5 | ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
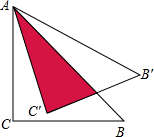 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是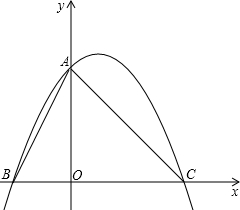
 如图,将直角边长为3cm的等腰Rt△ABC绕点A逆时针旋转15°得到△ADE,ED交AB于点F,则△AEF的面积为
如图,将直角边长为3cm的等腰Rt△ABC绕点A逆时针旋转15°得到△ADE,ED交AB于点F,则△AEF的面积为