题目内容
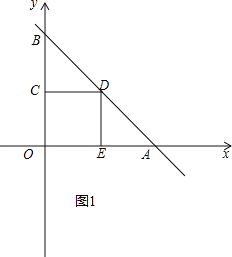
【题目】在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,则此正方形落在x轴正半轴的顶点坐标为 .
【答案】(1.5,0)或(1,0).
【解析】
试题分析:分两种情况:①如图1,令x=0,则y=3,令y=0,则x=3,得到OA=OB=3,∠BAO=45°,根据DE⊥OA,推出DE=AE,由于四边形COED是正方形,得到OE=DE,等量代换得到OE=AE,即可得到结论;②如图2,由(1)知△OFC,△EFA是等腰直角三角形,由四边形CDEF是正方形,得到EF=CF,于是得到AF=![]() ×
×![]() OF=2OF,求出OA=OF+2OF=3,即可得到结论.
OF=2OF,求出OA=OF+2OF=3,即可得到结论.
解:分两种情况;
①如图1,令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=![]() OA=1.5,
OA=1.5,
∴E(1.5,0);
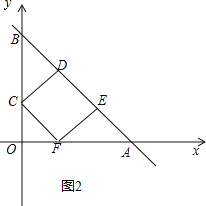
②如图2,由①知△OFC,△EFA是等腰直角三角形,
∴CF=![]() OF,AF=
OF,AF=![]() EF,
EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=![]() ×
×![]() OF=2OF,
OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
故答案为(1.5,0)或(1,0).

练习册系列答案
相关题目
【题目】张华记录了今年雨季钱塘江一周内水位变化的情况如下表(正号表示比前一天高,负号表示比前一天低):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化(m) | +0.25 | +0.80 | ﹣0.40 | +0.03 | +0.28 | ﹣0.36 | ﹣0.04 |
(1)本周星期 水位最高,星期 水位最低.
(2)与上周末相比,本周日的水位是上升了还是下降了?(写出计算过程)
(2)请用折线统计图表示钱塘江一周内水位变化的情况.