题目内容
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.

【答案】(1)抛物线的表达式为y=x2+2x﹣3;
(2)y的取值范围是﹣4≤y<5;
(3)b的取值范围是3<b<![]() .
.
【解析】试题分析:(1)把点(1,0)代入y=x2+mx+2m﹣7即可求得m的值,从而得二次函数的解析式;(2)求出当x=﹣1时和当x=﹣4时时y的值,根据函数的增减性确定y的取值范围;(3)把抛物线y=x2+2x﹣3的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=![]() .结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<
.结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<![]() .
.
试题解析:
(1)∵二次函数y=x2+mx+2m﹣7的图象经过点(1,0),
∴1+m+2m﹣7=0,解得m=2,
∴抛物线的表达式为y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4,
∵当﹣4<x<﹣1时,y随x增大而减小;
当﹣1≤x<1时,y随x增大而增大,
∴当x=﹣1,y最小=﹣4,
当x=﹣4时,y=5,
∴﹣4<x<1时,y的取值范围是﹣4≤y<5;
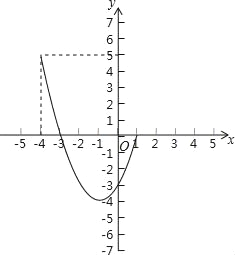
(3)y=x2+2x﹣3与x轴交于点(﹣3,0),(1,0),翻折后可得新图象M如图中红色部分,
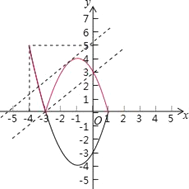
把抛物线y=x2+2x﹣3=(x+1)2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣(x+1)2+4(﹣3≤x≤1),
当直线y=x+b经过(﹣3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=﹣(x+1)2+4(﹣3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即﹣(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=![]() .
.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).