Question

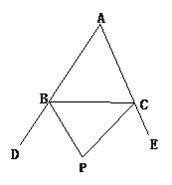
【题目】如图，PB和PC是△ABC的两条外角平分线。

①求证：∠BPC=90°-∠BAC．

②根据第①问的结论猜想：三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形？

Answer 1

【答案】①证明见解析②锐角三角形

【解析】试题分析: ①根据三角形的内角和定理、角平分线定义和三角形的外角的性质即可证明；

②根据①的结论，知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角，则该三角形是锐角三角形．

试题解析:

①证明：∵PB和PC是△ABC的两条外角平分线，

∴∠P=180°(∠PBC+∠PCB)=180° (∠CBD+∠BCE)=180° (∠A+∠ACB+∠BCE)=180° (∠A+180°)=90°∠A；

②根据①的结论，知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角，

三个角都是锐角的三角形是锐角三角形，故该三角形是锐角三角形。