��Ŀ����
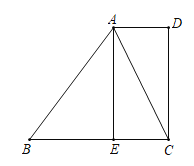
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ��12����B��ʾ12����C��ʾ20�����dzƵ�A�͵�C�����������32�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룬�ʣ�
��1������Q�ӵ�C�˶�����A��Ҫ�� ���룻
��2��P��Q��������ʱ�����t��ֵ��������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��A��P���������������ij�����C��Q���������������ij��ȵ�![]() ������P���˶���·�̣�
������P���˶���·�̣�![]() Q���˶���·�̣���
Q���˶���·�̣���
���𰸡���1��26�룻��2��t��ֵ��10��������M����Ӧ������8����3��26
��������
��1����ʱ��=·�̡��ٶȼ��ɽ��
��2����������ʱ��P��Q����ʱ����ȵĵ�����ϵ���з��̡��ⷽ�̼��ɽ��
��3��A��P���������������ij�����C��Q���������������ij��ȵ�![]() �������ֱ�DZ߷ֱ�������ۣ�������P���˶���·�̣�
�������ֱ�DZ߷ֱ�������ۣ�������P���˶���·�̣�![]() Q���˶��ĵ�����ϵ���з��̡��ⷽ�̼��ɽ��
Q���˶��ĵ�����ϵ���з��̡��ⷽ�̼��ɽ��
�⣺��1����Q�˶�����Aʱ������ʱ��t����20��12����1+12��2+12��1��26���룩��
�𣺶���Q�ӵ�C�˶�����A��Ҫ26�룻
��2�������֪��P��Q�����������߶�OB��M������OM��x��
��12��2+x��2����20��12����1+��12��x����2��
���x��8��
12��2+x��2��12��2+8��2��6+4��10��
��t��ֵ��10��������M����Ӧ������8��
��3��A��P���������������ij�����C��Q���������������ij��ȵ�![]() ����2�ֿ��ܣ�
����2�ֿ��ܣ�
�ٶ���Q��OB�ϣ�����P��AO�ϣ�
��2t��![]() [20��12+2��t��8��1��]��
[20��12+2��t��8��1��]��
��ã�t��20����ȥ����
�ڶ���Q��OA�ϣ�����P��BC�ϣ�
��2t��![]() [20+��t��8��1��12��2��]��
[20+��t��8��1��12��2��]��
��ã�t��10����ȥ����
����������t�⣮
�ʴ�Ϊ��26��

����Ŀ�������Ӱڳɵ���![]() ������ͼ����ͼ��ʾ��
������ͼ����ͼ��ʾ��
 ����
����
(1)������
ͼ����� | �� | �� | �� | �� | �� | �� |
ÿ��ͼ�������ӵĸ��� |
|
| ______ | _____ | �� | ______ |
(2)���![]() ����
����![]() ������ͼ�������ӵĸ���(�ú�
������ͼ�������ӵĸ���(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
(3)��20����![]() ������ͼ���������Ӷ��ٸ���
������ͼ���������Ӷ��ٸ���
����Ŀ���ס���������5�δ�в��������еĻ������£�
�ף�8��8��7��8��9
�ң�5��9��7��10��9
��1��������
ƽ���� | ���� | ��λ�� | ���� | |
�� | 8 | | 8 | 0.4 |
�� | | 9 | | 3.2 |
��2������������5�γɼ���ѡ��ײμ����������������������ʲô��
��3������������1�Σ�����8������ô�ҵ�����ɼ��ķ��� �������������������С����������������