题目内容
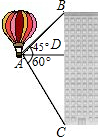如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为50m，求这栋楼的高度．（| 2 |
| 3 |
分析：求这栋楼的高度，即BC的长度，又因为BC=BD+DC，所以分别求出BD，CD就可以．
解答：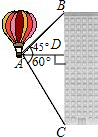
解：在Rt△ABD中，∠BDA=90°，∠BAD=45°，
∴BD=AD=50（m）．
在Rt△ACD中，∠ADC=90°，∠CAD=60°，
∴CD=
AD=50
（m）．
∴BC=BD+CD=50+50
=50(
+1)≈136.6（m）．
答：这栋楼约高136.6m．
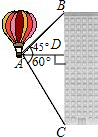解：在Rt△ABD中，∠BDA=90°，∠BAD=45°，∴BD=AD=50（m）．
在Rt△ACD中，∠ADC=90°，∠CAD=60°，
∴CD=
| 3 |
| 3 |
∴BC=BD+CD=50+50
| 3 |
| 3 |
答：这栋楼约高136.6m．
点评：此题主要考查了仰角俯角问题，以及利用三角函数关系解直角三角形，题目难度不大，是中考中常考题型．
练习册系列答案
相关题目
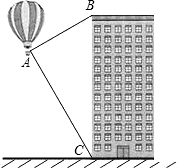如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，热气球与高楼的水平距离为66 m，这栋高楼有多高？（结果精确到0.1 m，参考数据：
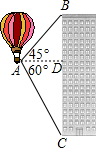如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为50m，则这栋楼的高度为
（2013•德阳）如图，热气球的探测器显示，从热气球A看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为60°，热气球A与高楼的水平距离为120m，这栋高楼BC的高度为（ ）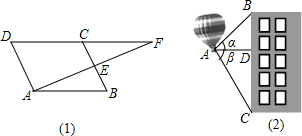
（2012•福州质检）（1）如图，在平行四边形ABCD中，E为BC中点，AE和延长线与DC的延长线相交于点F．证明：△ABE≌△FCE．