��Ŀ����
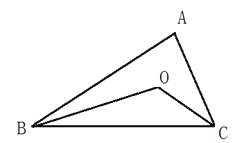
����Ŀ�������10�֣�AB��AC �ཻ�ڵ�A�� BD��CD�ཻ�ڵ�D��̽����BDC���B �� ��C����BAC�Ĺ�ϵ��
��������������
�����Ե�AΪ�˵�������AD��
�ߡ�1�ǡ�ABD����������1= ��B+��BAD��
ͬ����2=��C+��CAD��
���1+��2=��B+��BAD+��C+��CAD������BDC=��B+��C+��BAC��
СӢ��˼·�����ӳ�BD��AC�ڵ�E��
��1����СӢ��˼·��ɡ�BDC=��B+��C+��BAC��һ���ۣ�



��2�����������˼·���������������ͼ���ڡ�ABC����BE��CD�ֱ��ǡ�ABC��ACB�Ľ�ƽ��������AC��E����AB��D��BE��CD�ཻ�ڵ�O����A=60�������BOC�Ķ�����

��3����ͼ����ABC����BO��CO�ֱ��ǡ�ABC���ACB�Ľ�ƽ��������BO��CO�ཻ�ڵ�O�������BOC���A�������Ĺ�ϵ��������֤����
���𰸡���1��֤������������2��120������3����BOC=90��+ ![]() ��A��
��A��
�����������������
��1����СӢ��˼·����BDC�ǡ�DCE����ǣ���DEC�ǡ�ABE����ǣ�������������ǵ����ʿɵã���BDC=��C+��DEC����DEC=��B+��BAC���ɴ˿ɵã���BDC=��C+��B+��BAC��
��2������ABC����BE��CD�ֱ�����ABC��ACB�Ľ�ƽ��������AC��E����AB��D��BE��CD�ཻ�ڵ�O���ɵ���ABO+��ACO=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=60����
��180��-��A��=60����
������1���ɵá�BOC=��ABO+��ACO+��A=120����
��3���ɣ�2���ɵã���ABO+��ACO=![]() ��180��-��A��=90��-
��180��-��A��=90��-![]() ��A�����ɣ�1���ɵã���BOC=��ABO+��ACO+��A=90��-
��A�����ɣ�1���ɵã���BOC=��ABO+��ACO+��A=90��-![]() ��A+��A=90��+
��A+��A=90��+![]() ��A.
��A.
���������
��1���ӳ�BD��AC��E��
�ߡ�BDC= ��C+��CED����CED=��BAC+��B��
���BDC=��C+��B+��BAC��
��2���ߡ�ABC����BE��CD�ֱ��ǡ�ABC��ACB�Ľ�ƽ������
���ABE=![]() ��ABC����ACD=
��ABC����ACD=![]() ��ACB��
��ACB��
���ABE+��ACD=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=60����
��180��-��A��=60����
�ɣ�1��֪��BOC=��ABE+��ACD+��A
���BOC=60��+60��=120����
��3����BOC����A�Ĺ�ϵ����BOC=90��+![]() ��A������������
��A������������
�ߡ�ABC����BO��CO�ֱ��ǡ�ABC��ACB�Ľ�ƽ������
���ABO=![]() ��ABC����ACO=
��ABC����ACO=![]() ��ACB��
��ACB��
���ABO+��ACO=![]() ����ABC+��ACB��=
����ABC+��ACB��=��180��-��A��=90��-
![]() ��A��
��A��
��������1����֪����BOC=��ABO+��ACO+��A��
���BOC=90��-![]() ��A+��A=90��+
��A+��A=90��+![]() ��A.
��A.


