题目内容
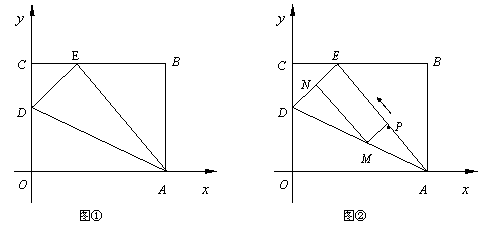
如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在![]() 轴的正半轴上,点C在
轴的正半轴上,点C在![]() 轴的正半轴上,OA=5,OC=4.
轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标;
(2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为秒![]() ,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式;当取何值时,S有最大值?最大值是多少?
,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式;当取何值时,S有最大值?最大值是多少?
(3)在(2)的条件下,当为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标.
 |
解:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∴![]() 点坐标为
点坐标为![]() ………………………………………………………(1分)
………………………………………………………(1分)
在![]() 中,
中,![]() 又∵
又∵![]()
∴![]() 解得:
解得:![]()
∴![]() 点坐标为
点坐标为![]() ………………………………………………………(2分)
………………………………………………………(2分)
(2)如图①∵![]() ∥
∥![]() ∴
∴![]()
![]()
∴![]() 又知
又知![]()
∴![]() 又∵
又∵![]()
而显然四边形![]() 为矩形
为矩形
∴![]() …………………(3分)∴
…………………(3分)∴![]() 又∵
又∵![]()
∴当![]() 时,
时,![]() 有最大值
有最大值![]() (面积单位)
(面积单位)
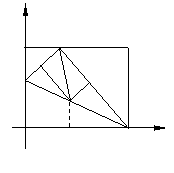
(3)(i)若![]() (如图①)
(如图①)
在![]() 中,
中,![]() ,
,![]() ∴
∴![]() 为
为![]() 的中点
的中点
又∵![]() ∥
∥![]() , ∴
, ∴![]() 为
为![]() 的中点
的中点
 ∴
∴![]() ∴
∴![]() ∴
∴![]()
又∵![]() 与
与![]() 是关于
是关于![]() 对称的两点
对称的两点
∴![]() ,
,![]()
∴当![]() 时(
时(![]() ),
),![]() 为等腰三角形
为等腰三角形
此时![]() 点坐标为
点坐标为![]()
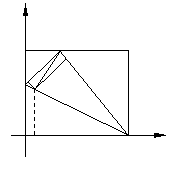 (ii)若
(ii)若![]() (如图②)
(如图②)
在![]() 中,
中,![]()
∵![]() ∥
∥![]() ,∴
,∴![]()
![]() ,∴
,∴![]()
∴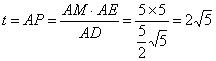 ∴
∴![]()
同理可知:![]() ,
, ![]()
∴当![]() 时(
时(![]() ),此时
),此时![]() 点坐标为
点坐标为![]()
综合(i)、(ii)可知:![]() 或
或![]() 时,以A、M、E为顶点的三角形为等腰三角形,相应M点的坐标为
时,以A、M、E为顶点的三角形为等腰三角形,相应M点的坐标为![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在边OA的点D处.已知折叠CE=5
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在边OA的点D处.已知折叠CE=5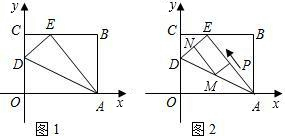
 ,使点B落在边OA的点D处.已知折痕CE=
,使点B落在边OA的点D处.已知折痕CE= 在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点. 如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.
如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.