题目内容
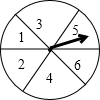
 (1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗?
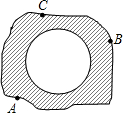
(1)如图所示的转盘中指针落在每个数字上的机会相等,现同时转动A、B两转盘,停止后,指针各指向一个数字.小彬和小颖利用这个转盘做游戏:若两数之积为非负数则小彬胜,否则,小颖胜.你认为这个游戏对双方公平吗?(2)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
| 掷石子次数 石子落在的区域 |
50次 | 150次 | 300次 |
| 石子落在 |
14 | 43 | 93 |
| 石子落在阴影内的次数n | 19 | 85 | 186 |
分析:(1)本题考查概率问题中的公平性问题,解决本题的关键是计算出各种情况的概率,然后比较即可.
(2)根据统计表,计算出石子落在圆内的概率,即圆面积与总面积的比值,从而可计算出图形ABC的面积.
(2)根据统计表,计算出石子落在圆内的概率,即圆面积与总面积的比值,从而可计算出图形ABC的面积.
解答:解:(1)根据题意分析可得:同时转动A、B两转盘,选取的数字不同可分为12种情况,其中积为的负数有5种,为0的有3种,为正数的有4种;若两数之积为非负数则小彬胜,即小彬胜的概率为
,则小颖胜的概率为
;故游戏不公平.
(2)根据统计表,可得石子落在圆内的概率与落在阴影部分的概率之比为:
=
,
圆的面积=π•12=π,
设阴影图形的面积为x,则有
=
,
解得x=2π.
∴封闭图形ABC的面积=π+2π=3π.
| 7 |
| 12 |
| 5 |
| 12 |
(2)根据统计表,可得石子落在圆内的概率与落在阴影部分的概率之比为:
| 93 |
| 186 |
| 1 |
| 2 |
圆的面积=π•12=π,
设阴影图形的面积为x,则有
| π |
| x |
| 1 |
| 2 |
解得x=2π.
∴封闭图形ABC的面积=π+2π=3π.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用力旋转如图所示的转盘甲和转盘乙的指针,如果想让指针停在黑色上面,选取哪个转盘成功的机会比较大( )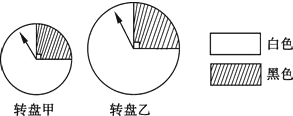

| A、转盘甲 | B、转盘乙 | C、两个一样大 | D、无法确定 |