题目内容
 (2012•白下区一模)写出下列命题的已知、求证,并完成证明过程.
(2012•白下区一模)写出下列命题的已知、求证,并完成证明过程.命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:如图,
在□ABCD中,对角线AC平分∠DAB(或∠DCB)
在□ABCD中,对角线AC平分∠DAB(或∠DCB)
.求证:
□ABCD是菱形
□ABCD是菱形
.证明:
分析:把原命题的题设作为已知,把原命题的结论作为求证即可,再根据根据一条对角线平分一个内角,则有这两个角相等.根据两直线平行内错角相等,得出一个三角形两个内角相等,即两边相等,根据菱形的概念:有一组邻边相等的平行四边形是菱形即证.
解答:命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:在四边形ABCD中,对角线AC平分∠DAB(或∠DCB).
求证:四边形ABCD是菱形,
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠BCA.
∵对角线AC平分∠DAB,
∴∠DAC=∠BAC.
∴∠BCA=∠BAC.
∴BA=BC.
∴四边形ABCD是菱形.
已知:在四边形ABCD中,对角线AC平分∠DAB(或∠DCB).
求证:四边形ABCD是菱形,
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠BCA.
∵对角线AC平分∠DAB,
∴∠DAC=∠BAC.
∴∠BCA=∠BAC.
∴BA=BC.
∴四边形ABCD是菱形.
点评:此题主要考查菱形的判定方法,解题的关键是熟记各种菱形的各种判定方法.

练习册系列答案
相关题目
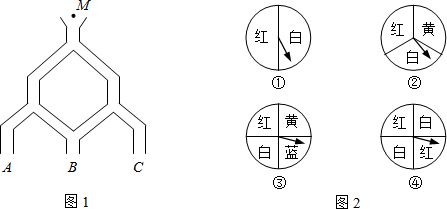
 (2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=
(2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=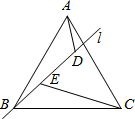 (2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=
(2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=