题目内容
“元旦大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“谢谢”、“10元”、“20元”和“30元”的字样.规定:在本商场同一日内,顾客每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券.某顾客刚好消费200元.
(1)该顾客至多可得到多少元购物券?
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
解:(1)∵该顾客刚好消费200元,
∴该顾客可以在箱子里先后摸出两个球,
∴该顾客至多可得到30+20=50(元)购物券;
(2)根题意列表如下:
| 0元 | 10元 | 20元 | 30元 | |
| 0元 | (0,10) | (0,20) | (0,30) | |
| 10元 | (10,0) | (10,20) | (10,30) | |
| 20元 | (20,0) | (20,10) | (20,30) | |
| 30元 | (30,0) | (30,10) | (30,20) |
因为顾客从箱子中先后摸出两个球,共有12种等可能出现的结果,其中顾客所获得购物券的金额不低于30元共有8种结果,
所以P(不低于30元)=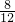 =
= .
.
分析:(1)先根据顾客刚好消费200元,求出该顾客可以在箱子里先后摸出两个球,再求出这两个球的最大和即可;
(2)根据题意列出表,求出该顾客所获得购物券的金额不低于30元的情况数和总的情况数,再根据概率公式进行计算即可.
点评:此题考查了列表法和概率公式,解题的关键是掌握列表法求概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目