题目内容
把长为8cm的矩形按虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是（ ）
A、（10+2
| ||
B、（10+
| ||
| C、22cm | ||
| D、18cm |
分析：根据剪去的三角形的面积可得矩形的宽，利用勾股定理即可求得等腰梯形的腰长，根据折叠可得梯形其余边长，相加即为梯形的周长．
解答：解：∵剪掉部分的面积为6cm2，
∴矩形的宽为2，
易得梯形的下底为矩形的长，上底为（8÷2-3）×2=2，腰长为
=
，
∴打开后梯形的周长是（10+2
）cm．
故选：A．
∴矩形的宽为2，
易得梯形的下底为矩形的长，上底为（8÷2-3）×2=2，腰长为
| 22+32 |
| 13 |
∴打开后梯形的周长是（10+2
| 13 |
故选：A．
点评：此题主要考查了学生对等腰梯形的性质及翻折掌握情况，解决本题的关键是根据折叠的性质得到等腰梯形的各边长．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
把长为8cm的矩形按虚线对折，按图中虚线剪出一个直角梯形，展开得到一个等腰梯形，剪掉部分的面积为12cm2，则打开后梯形的周长是多少cm（ ）
| A、32 | ||
| B、15 | ||
C、2
| ||
| D、20 |
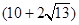cm B．
cm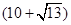 C．22cm D．18cm
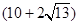cm
B．
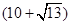cm
C．22cm D．18cm