题目内容
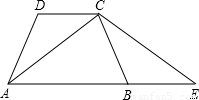
(2009•通州区一模)如图,在三角形ABC中,AC=BC,若将△ABC沿BC方向向右平移BC长的距离,得到△CEF,连接AE.(1)试猜想,AE与CF有何位置上的关系?并对你的猜想给予证明;
(2)若BC=10,tan∠ACB=
 时,求AB的长.
时,求AB的长.
【答案】分析:(1)由平移可得,∠ACB=∠FEC,AC=CE=EF=AF,那么四边形ACEF是菱形,由邻边相等可得到是菱形,所以对角线互相垂直;
(2)作出BC边上高AD,利用AC,及tan∠ACB的值,求得AD,CD长,进而得到BD长,利用勾股定理求解即可.
解答: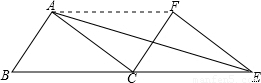 解:(1)AE⊥CF
解:(1)AE⊥CF
证明:如图,连接AF,
∵AC=BC,
又∵△ABC沿BC方向向右平移BC长的距离,
∴AC=CE=EF=AF.
∴四边形ACEF是菱形.
∴AE⊥CF.
(2)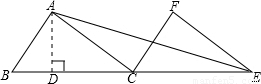 如图,作AD⊥BC于D
如图,作AD⊥BC于D
∵tan∠ACB= ,
,
设AD=3KDC=4K,
在Rt△ADC中,AC=10,
∵AD2+DC2=AC2
∴K=2.
∴AD=6cm,DC=8cm.
∴BD=2cm.
在Rt△ADB中,根据勾股定理:AB=2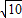 c.
c.
点评:平移前后对应线段,对应角相等,作高构造已给三角函数所在的直角三角形是常用的辅助线作法.
(2)作出BC边上高AD,利用AC,及tan∠ACB的值,求得AD,CD长,进而得到BD长,利用勾股定理求解即可.
解答:
 解:(1)AE⊥CF
解:(1)AE⊥CF证明:如图,连接AF,
∵AC=BC,
又∵△ABC沿BC方向向右平移BC长的距离,
∴AC=CE=EF=AF.
∴四边形ACEF是菱形.
∴AE⊥CF.
(2)
 如图,作AD⊥BC于D
如图,作AD⊥BC于D∵tan∠ACB=
 ,
,设AD=3KDC=4K,
在Rt△ADC中,AC=10,
∵AD2+DC2=AC2
∴K=2.
∴AD=6cm,DC=8cm.
∴BD=2cm.
在Rt△ADB中,根据勾股定理:AB=2
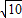 c.
c.点评:平移前后对应线段,对应角相等,作高构造已给三角函数所在的直角三角形是常用的辅助线作法.

练习册系列答案
相关题目
(2009•通州区一模)下表给出了代数式x2+bx+c与x的一些对应值:
(1)根据表格中的数据,确定b、c的值,并填齐表格空白处的对应值;
(2)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.
| x | … | -1 | 1 | 2 | 3 | 4 | … | |
| x2+bx+c | … | 3 | -1 | 3 | … |
(2)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y轴交于点C,P为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.

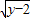 =0,则x+2y的值为( )
=0,则x+2y的值为( )