题目内容
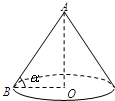某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB与底面半径OB的夹角为α，tanα=| 4 | 3 |
分析：由圆锥高为8，母线AB与底面半径OB的夹角为α，tanα=
，利用解直角三角形得出BO的长，再由勾股定理求得圆锥的母线长后，利用圆锥的侧面面积公式求出．
| 4 |
| 3 |
解答：解：∵AO=8米，母线AB与底面半径OB的夹角为α，tanα=
，
∴tanα=
=
=
，
∴BO=6，∴AB=10，
根据圆锥的侧面积公式：πrl=π×6×10=60π，
故答案为：60π．
| 4 |
| 3 |
∴tanα=
| 4 |
| 3 |
| AO |
| BO |
| 8 |
| BO |
∴BO=6，∴AB=10，
根据圆锥的侧面积公式：πrl=π×6×10=60π，
故答案为：60π．
点评：此题主要考查了圆锥侧面积公式，根据已知得出BO=6，AB=10，再利用圆锥侧面积公式求出是解决问题的关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
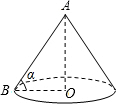某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB与底面半径OB的夹角为α，
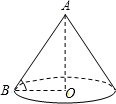某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB=10米，则该圆锥的侧面积是
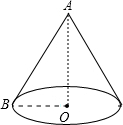某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，底面半径0B=6米，则圆锥的侧面积是
（2012•开平区一模）某盏路灯照射的空间可以看成如图所示的圆椎，它的高AO=