题目内容
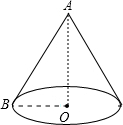 某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,底面半径0B=6米,则圆锥的侧面积是
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,底面半径0B=6米,则圆锥的侧面积是分析:根据勾股定理求得OB,再求得圆锥的底面周长即圆锥的侧面弧长,根据扇形面积的计算方法S=
lr,求得答案即可.
| 1 |
| 2 |
解答:解:∵AO=8米,OB=6米,∴AB=10米,
∴圆锥的底面周长=2×π×6=12π米,
∴S扇形=
lr=
×12π×10=60π米2.
故答案为:60π.
∴圆锥的底面周长=2×π×6=12π米,
∴S扇形=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:60π.
点评:本题考查了圆锥的有关计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
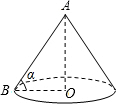 某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,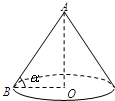 某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,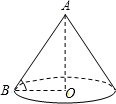 某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB=10米,则该圆锥的侧面积是
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB=10米,则该圆锥的侧面积是 (2012•开平区一模)某盏路灯照射的空间可以看成如图所示的圆椎,它的高AO=
(2012•开平区一模)某盏路灯照射的空间可以看成如图所示的圆椎,它的高AO=