题目内容
(2013•顺义区二模)问题:如果存在一组平行线a∥b∥c,请你猜想是否可以作等边三角形ABC使其三个顶点分别在a、b、c上?
小明同学的解答如下:如图1所示,过点A作AM⊥b于M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线c于点C,在直线b上取点B使BM=CN,则△ABC为所求.
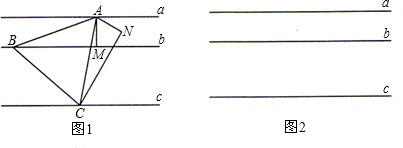
(1)请你参考小明的作法,在图2中作一个等腰直角三角形DEF使其三个顶点分别在a、b、c上,点D为直角顶点;
(2)若直线a、b之间的距离为1,b、c之间的距离为2,则在图2中,S△DEF=
.
小明同学的解答如下:如图1所示,过点A作AM⊥b于M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线c于点C,在直线b上取点B使BM=CN,则△ABC为所求.
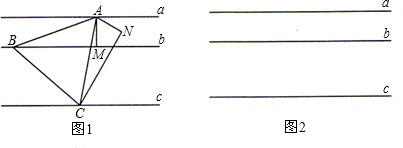
(1)请你参考小明的作法,在图2中作一个等腰直角三角形DEF使其三个顶点分别在a、b、c上,点D为直角顶点;
(2)若直线a、b之间的距离为1,b、c之间的距离为2,则在图2中,S△DEF=
5
5
,在图1中AC=| 2 |
| 3 |
| 21 |
| 2 |
| 3 |
| 21 |
分析:(1)在a上取一点D,作DH⊥b于H,在a上取点M使DM=DH,作MF⊥DM于M交c于点F,在b上取一点E使HE=MF,连接DE,DF,EF,则△DEF是所求作的三角形;
(2)由作图可以由勾股定理得出DF的值,在图1中,过点N作HG⊥a于H,交c于点G,由勾股定理先求出CN的值就可以求出AC的值.
(2)由作图可以由勾股定理得出DF的值,在图1中,过点N作HG⊥a于H,交c于点G,由勾股定理先求出CN的值就可以求出AC的值.
解答:解:(1)如图2,①在a上取一点D,作DH⊥b于H,
②在a上取点M使DM=DH,
③作MF⊥DM于M交c于点F,
④在b上取一点E使HE=MF,
⑤连接DE,DF,EF,
∴△DEF是所求作的三角形.
(2)∵a、b之间的距离为1,b、c之间的距离为2,
∴DM=DH=1,MF=1+2=3.
在Rt△FDM中,由勾股定理,得
DF=
=
.
∴S△DEF=
×(
)2=5.
如图1,过点N作HG⊥a于H,交c于点G,
∴∠AHN=∠NGC=90°.
∵∠MAN=60°,
∴∠HAN=30°,
∴HN=
AN.∠ANH=60°.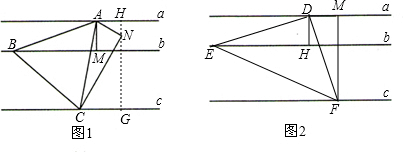
∵AM=AN=1,
∴HN=0.5.
∴HG=2.5.
∵CN⊥AN,
∴∠ANC=90°,
∴∠ANH+∠CNG=90°,
∴∠CNG=30°,
∴CN=2CG,
在Rt△CGN中,由勾股定理,得
4CG2-CG2=
,
CG=
,
∴CN=
.
在Rt△ANC中,由勾股定理,得
AC2=(
)2+1,
∴AC=
.
故答案为:5,
.
②在a上取点M使DM=DH,
③作MF⊥DM于M交c于点F,
④在b上取一点E使HE=MF,
⑤连接DE,DF,EF,
∴△DEF是所求作的三角形.
(2)∵a、b之间的距离为1,b、c之间的距离为2,
∴DM=DH=1,MF=1+2=3.
在Rt△FDM中,由勾股定理,得
DF=
| 1+9 |
| 10 |
∴S△DEF=
| 1 |
| 2 |
| 10 |
如图1,过点N作HG⊥a于H,交c于点G,
∴∠AHN=∠NGC=90°.
∵∠MAN=60°,
∴∠HAN=30°,
∴HN=
| 1 |
| 2 |
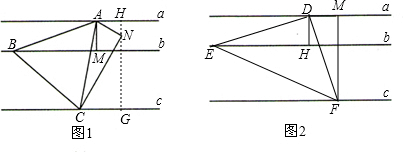
∵AM=AN=1,
∴HN=0.5.
∴HG=2.5.
∵CN⊥AN,
∴∠ANC=90°,
∴∠ANH+∠CNG=90°,
∴∠CNG=30°,
∴CN=2CG,
在Rt△CGN中,由勾股定理,得
4CG2-CG2=
| 25 |
| 4 |
CG=
| 5 |
| 6 |
| 3 |
∴CN=
| 5 |
| 3 |
| 3 |
在Rt△ANC中,由勾股定理,得
AC2=(
| 5 |
| 3 |
| 3 |
∴AC=
| 2 |
| 3 |
| 21 |
故答案为:5,
| 2 |
| 3 |
| 21 |
点评:本题考查了作图的运用,等腰直角三角形的性质的运用,勾股定理的运用,直角三角形的性质的运用,全等三角形的性质的运用,解答时合理运用全等三角形的性质是关键.

练习册系列答案
相关题目