题目内容
已知在?ABCD中,AB=40cm,BC=25cm,∠ABC=120°,求?ABCD的两条高和面积.分析:关键平行四边形的性质求出AD=25cm,∠A=60°,过点D作DE⊥AB,E为垂足,过点B作BF⊥AD,F为垂足,根据锐角三角函数求出高DE、BF即可,根据平行四边形的面积公式求出面积即可.
解答: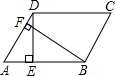 解:∵平行四边形ABCD,AB=40cm,BC=25cm,∠ABC=120°,
解:∵平行四边形ABCD,AB=40cm,BC=25cm,∠ABC=120°,
∴AD∥BC,AD=BC,
∴AD=25cm,∠A=60°,
过点D作DE⊥AB,E为垂足,
过点B作BF⊥AD,F为垂足,
则DE=AD•sinA=25×
=
(cm),
BF=AB•sinA=40×
=20
(cm),
S平行四边形ABCD=AB×DE=40cm×
cm=500
cm2.
答:?ABCD的两条高是
cm2,20
cm2,面积是500
cm2.
 解:∵平行四边形ABCD,AB=40cm,BC=25cm,∠ABC=120°,
解:∵平行四边形ABCD,AB=40cm,BC=25cm,∠ABC=120°,∴AD∥BC,AD=BC,
∴AD=25cm,∠A=60°,
过点D作DE⊥AB,E为垂足,
过点B作BF⊥AD,F为垂足,
则DE=AD•sinA=25×
| ||
| 2 |
| 25 |
| 2 |
| 3 |
BF=AB•sinA=40×
| ||
| 2 |
| 3 |
S平行四边形ABCD=AB×DE=40cm×
| 25 |
| 2 |
| 3 |
| 3 |
答:?ABCD的两条高是
| 25 |
| 2 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查对平行四边形的性质,解直角三角形等知识点的理解和掌握,能正确解直角三角形是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

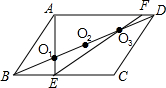 (1997•河北)如图,已知在?ABCD中,O1、O2、O3为对角线BD上三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则AD:FD等于( )
(1997•河北)如图,已知在?ABCD中,O1、O2、O3为对角线BD上三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则AD:FD等于( ) 如图,已知在?ABCD中,∠A=154°,则∠B等于( )
如图,已知在?ABCD中,∠A=154°,则∠B等于( )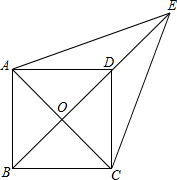 如图,已知在?ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
如图,已知在?ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.