题目内容
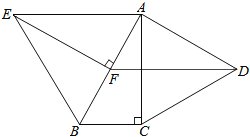
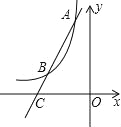
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 ![]() ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.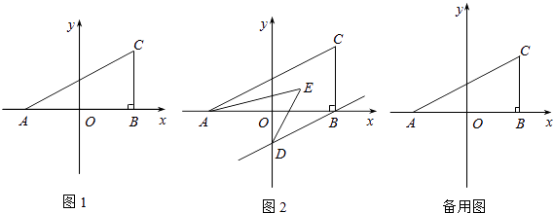
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
【答案】
(1)
解:∵(a+2)2+ ![]() =0,
=0,
∴a=2=0,b﹣2=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2),
∴△ABC的面积= ![]() ×2×4=4
×2×4=4
(2)
解:∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF∥AC,如图①,
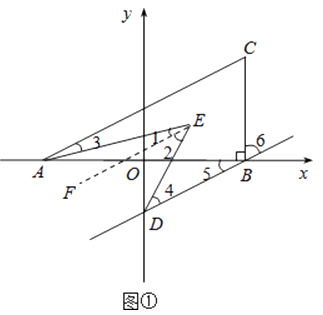
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,
∠ODB=∠2,
∴∠AED=∠1+∠2= ![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
(3)
解:①当P在y轴正半轴上时,如图②,
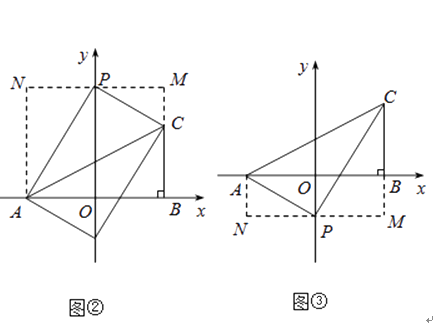
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4,
∴ ![]() ﹣t﹣(t﹣2)=4,解得t=3,
﹣t﹣(t﹣2)=4,解得t=3,
②当P在y轴负半轴上时,如图③
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4
∴ ![]() +t﹣(2﹣t)=4,解得t=﹣1,
+t﹣(2﹣t)=4,解得t=﹣1,
∴P(0,﹣1)或(0,3)
【解析】(1)根据非负数的性质易得a=﹣2,b=2,然后根据三角形面积公式计算;(2)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,所以∠AED=∠1+∠2=
∠ODB=∠2,所以∠AED=∠1+∠2= ![]() (∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
当P在y轴负半轴上时,运用同样方法可计算出t.
【考点精析】掌握平行线的判定与性质和三角形的面积是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的面积=1/2×底×高.

【题目】甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环2) | 0.035 | 0.016 | 0.022 | 0.025 |
则这四个人种成绩发挥最稳定的是( )
A.甲B.乙C.丙D.丁