题目内容
如图,已知一次函数y=-| 3 | 4 |
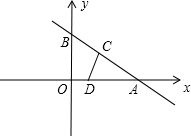 1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.
1个单位/s的速度从点B向A运动,同时点D在线段AO上以同样的速度从点A向O运动,运动时间用t(s)表示.(1)求AB的长;
(2)当t为何值时,△ACD和△AOB相似?
(3)求出(2)中当△ACD和△AOB相似时,CD所在直线的函数解析式.
分析:(1)由直线的解析式可求出A、B点的坐标,得到OA、OB的大小,利用勾股定理可求得AB的长;
(2)要求t的值,可根据相似得到比例式,代入数值求得t值;
(3)求出三角形相似时C、D的坐标,利用待定系数法求得答案.
(2)要求t的值,可根据相似得到比例式,代入数值求得t值;
(3)求出三角形相似时C、D的坐标,利用待定系数法求得答案.
解答: 解:(1)由已知得A(4,0),B(0,3)
解:(1)由已知得A(4,0),B(0,3)
∴OA=4,OB=3
∴AB=
=5.
(2)当
=
或
=
时两三角形相似,
即
=
或
=
解得t=
或t=
.
(3)当t=
时,直线CD的解析式为直线x=4-
=
,
当t=
时,直线CD的解析式为y=
x-
.
 解:(1)由已知得A(4,0),B(0,3)
解:(1)由已知得A(4,0),B(0,3)∴OA=4,OB=3
∴AB=
| 32+42 |
(2)当
| AC |
| AB |
| AD |
| AO |
| AC |
| OA |
| AD |
| AB |
即
| 5-t |
| 5 |
| t |
| 4 |
| 5-t |
| 4 |
| t |
| 5 |
解得t=
| 20 |
| 9 |
| 25 |
| 9 |
(3)当t=
| 20 |
| 9 |
| 20 |
| 9 |
| 16 |
| 9 |
当t=
| 25 |
| 9 |
| 4 |
| 3 |
| 44 |
| 27 |
点评:本题考查了一次函数的综合运用;第二、三小问的求解中,要注意分情况讨论,在做此类问题时要思考全面,不能遗漏.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
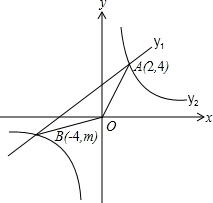 B(-4,m)两点.
B(-4,m)两点.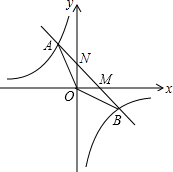 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数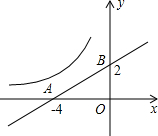 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数