Question

已知，如图，在平面直角坐标系中，以BC为直径的⊙M交x轴正半轴于点A、B，交y轴正半轴于点E、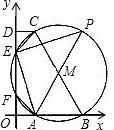F，过点C作CD垂直y轴，垂足为点D，连接AM并延长交⊙M于点P，连接PE．
（1）求证：∠FAO=∠EAM；
（2）若二次函数y=-x²+px+q的图象经过点B、C、E，且以C为顶点，当点B的横坐标等于2时，四边形OECB的面积是

11

4

，求这个二次函数的解析式．

Answer 1

分析：（1）根据四边形APEF是⊙M的内接四边形的性质可知∠APE=∠AFO，利用EAM=90°-∠APE，∠FAO=90°-∠AFO得到∠EAM=∠FAO；
（2）利用顶点公式可知C点的坐标(

p

2

，

p2+4q

4

)，图象过E点，得E点的坐标为（0，q），连接AC，OC，则AC⊥OB，CD⊥y轴，AO⊥OD，可证明四边形OACD为矩形，得到DC=OA，S_△OCB=

1

2

OB•AC=

1

2

×2×

4q+p2

4

=

4q+p2

4

，S_△OCE=

1

2

OE•CD=

1

2

q•

p

2

=

pq

4

，所以p²+pq+4q=11，把点B（2，0）代入可得2p+q-4=0，联立方程组解得p=1，q=2，所以过B、C、E三点的二次函数的解析式为y=-x²+x+2．

解答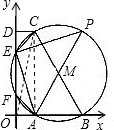：（1）证明：如图，
∵四边形APEF是⊙M的内接四边形
∴∠APE=∠AFO
∵AP为⊙M的直径
∴∠EAM=90°-∠APE
∵∠FAO=90°-∠AFO
∴∠EAM=∠FAO（3分）．

（2）解：因为二次函数y=-x²+px+q的图象的顶点为C点，
所以得C点的坐标(

p

2

，

p2+4q

4

)，
∵图象过E点，
∴得E点的坐标为（0，q）．（4分）
连接AC，则AC⊥OB，∵CD⊥y轴，AO⊥OD，
∴四边形OACD为矩形
∴DC=OA，连接OC，
S_△OCB=

1

2

OB•AC=

1

2

×2×

4q+p2

4

=

4q+p2

4

S_△OCE=

1

2

OE•CD=

1

2

q•

p

2

=

pq

4

∴

p2+4q+pq

4

=

11

4

即p²+pq+4q=11（6分）
∵点B（2，0）在抛物线y=-x²+px+q上
∴2p+q-4=0，联立

p2+pq+4q=11 2p+q-4=0

．
解这个方程组，得

p=1 q=2

&&

p=-5

（不合题意，舍去）
∴过B、C、E三点的二次函数的解析式为y=-x²+x+2．（9分）

点评：本题考查二次函数的综合应用，其中涉及到的知识点圆内接四边形的性质，二次函数顶点坐标求法以及函数的交点的意义等，要熟练掌握才能灵活运用．