题目内容
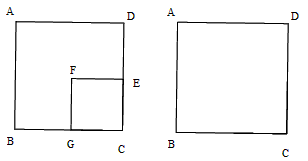
四边形ABCD和FGCE都是正方形，且CG和CE分别在CB和CD上，我们可以知道BG=DE，如果我们把正方形CGFE绕C点顺时钟旋转90度后，解决下列问题，
（1）画出旋转后的图形，并连结BG和DE。
（2）BG和DE的长度是否相等？说明理由。
（3）BG和DE有怎么样的位置关系？说明理由。
（4）把FGCE任意转动一个角度上面（2）（3）的结论是否仍然成立？
（1）画出旋转后的图形，并连结BG和DE。
（2）BG和DE的长度是否相等？说明理由。
（3）BG和DE有怎么样的位置关系？说明理由。
（4）把FGCE任意转动一个角度上面（2）（3）的结论是否仍然成立？
解：（1）旋转的图形如下图：
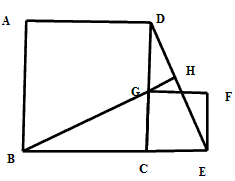
（2）∵四边形ABCD和四边形FGCD为正方形
∴∠BCG=∠ECD=90°，
BC=CD，CE=CG,
在△BCG和△DCE中
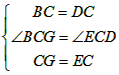
∴△BCD≌△DCE
∴BG=DE；
（3）∵△BCG≌△DCE
∴∠CBG=∠CDE
又∵∠CDE+∠DEC=90°，
∴∠EBH+∠HEB=90°，
∴∠BHE=90°，
∴BG⊥DE；
（4）结论仍然成立。
（2）∵四边形ABCD和四边形FGCD为正方形
∴∠BCG=∠ECD=90°，
BC=CD，CE=CG,
在△BCG和△DCE中
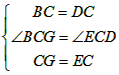
∴△BCD≌△DCE
∴BG=DE；
（3）∵△BCG≌△DCE
∴∠CBG=∠CDE
又∵∠CDE+∠DEC=90°，
∴∠EBH+∠HEB=90°，
∴∠BHE=90°，
∴BG⊥DE；
（4）结论仍然成立。
练习册系列答案
活力课时同步练习册系列答案
相关题目
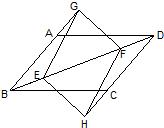28、如图，E、F是平行四边形ABCD对角线BD上两点，BE=DF，点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．四边形GEHF是平行四边形吗？为什么？
12、如图所示，在四边形ABCD中，AD∥BC，BC＞AD，∠B与∠C互余，将AB，CD分别平移到EF和EG的位置，则△EFG为
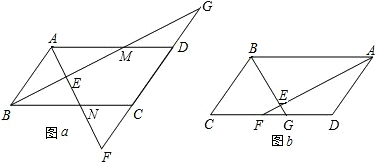
如图，四边形ABCD为正方形，曲线DEFGHIJ…叫做“正方形ABCD的渐开线”．其中