题目内容
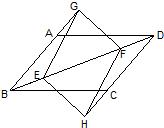 28、如图,E、F是平行四边形ABCD对角线BD上两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.四边形GEHF是平行四边形吗?为什么?
28、如图,E、F是平行四边形ABCD对角线BD上两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.四边形GEHF是平行四边形吗?为什么?分析:根据平行四边形的性质可得到AB=CD,∠ABE=∠CDF,已知BE=DF,AG=CH,可得到BG=DH,BF=DE,从而可以分别利用SAS来判定△BEG≌△DFH,△BGF≌△DHE,由全等三角形的对应边相等可得到GE=HF,GF=HE,即可根据两组边对应相等的四边形是平行四边形.
解答:解:法一、四边形GEHF是平行四边形.
∵四边形ABCD是平行四边形
∴AB=CD,∠ABE=∠CDF
∵BE=DF,AG=CH
∴BG=DH,BF=DE
∴△BEG≌△DFH,△BGF≌△DHE
∴GE=HF,GF=HE
∴四边形GEHF是平行四边形.
法二:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠GBE=∠HDF.
又∵AG=CH,
∴BG=DH.
又∵BE=DF,
∴△GBE≌△HDF.
∴GE=HF,∠GEB=∠HFD.
∴∠GEF=∠HFE.
∴GE∥HF.
∴四边形GEHF是平行四边形.
∵四边形ABCD是平行四边形
∴AB=CD,∠ABE=∠CDF
∵BE=DF,AG=CH
∴BG=DH,BF=DE
∴△BEG≌△DFH,△BGF≌△DHE
∴GE=HF,GF=HE
∴四边形GEHF是平行四边形.
法二:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠GBE=∠HDF.
又∵AG=CH,
∴BG=DH.
又∵BE=DF,
∴△GBE≌△HDF.
∴GE=HF,∠GEB=∠HFD.
∴∠GEF=∠HFE.
∴GE∥HF.
∴四边形GEHF是平行四边形.
点评:此题主要考查平行四边形的判定与性质及全等三角形的判定与性质的综合运用.

练习册系列答案
相关题目
 8、
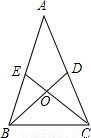
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
 相交于点C.
相交于点C.
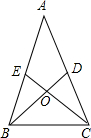 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.