题目内容
【题目】在平面直角坐标系xOy中,抛物线C:y=ax2﹣2ax+3与直线l:y=kx+b交于A,B两点,且点A在y轴上,点B在x轴的正半轴上.
(1)求点A的坐标;
(2)若a=﹣1,求直线l的解析式;
(3)若﹣3<k<﹣1,求a的取值范围.
【答案】(1)(0,3);(2)y=﹣x+3;(3)a<﹣1或a>3.
【解析】
(1)抛物线C:y=ax2﹣2ax+3与y轴交于点A,令x=0,即可求得A的坐标;
(2)令y=0,解方程即可求得B的坐标,然后根据待定系数法即可求得直线l的解析式;
(3)当a=3时,抛物线C过点B(1,0),此时k=﹣3.当a=﹣1时,抛物线C过点B(3,0),此时k=﹣1.结合图象即可求得.
解:(1)∵抛物线C:y=ax2﹣2ax+3与y轴交于点A,
∴点A的坐标为(0,3).
(2)当a=﹣1时,抛物线C为y=﹣x2+2x+3.
∵抛物线C与x轴交于点B,且点B在x轴的正半轴上,
∴点B的坐标为(3,0).
∵直线l:y=kx+b过A,B两点,
∴![]() 解得
解得 ![]()
∴直线l的解析式为y=﹣x+3.
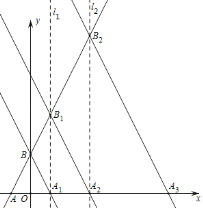
(3)如图,
当a>0时,
当a=3时,抛物线C过点B(1,0),此时k=﹣3.
结合函数图象可得a>3.
当a<0时,
当a=﹣1时,抛物线C过点B(3,0),此时k=﹣1.
结合函数图象可得a<﹣1.
综上所述,a的取值范围是a<﹣1或a>3.
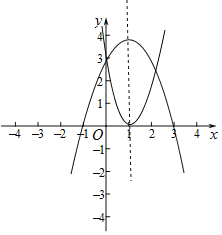

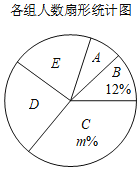
【题目】为了解初一同学们参加学校社团的情况,某班同学随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.其中A:英语演讲社团,B:语文阅读社团,C:数学思维训练社团,D:书法社团,E:天文社团.统计后知道:被调查的同学中数学思维训练社团的学生数是书法社团学生数的1.5倍.
各组人数统计表
组别 | 人数 |
A | 4 |
B | 6 |
C | a |
D | b |
E | 10 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有____人,m=____;
(2)求扇形统计图中扇形D的圆心角度数;
(3)该校共有1000人,请估计参加书法社团的人数.