题目内容
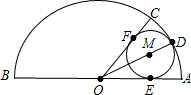 如图:有一个半径为R的半圆,要用这个半圆做一个圆锥的侧面和底面,小芳想这样做:在圆弧上取点C,使∠AOC=60°,用扇形OBC作圆锥的侧面,在扇形OAC内剪一个最大的⊙M作圆锥的底面,你认为小芳这样做办得到吗?请你通过计算说明理由.
如图:有一个半径为R的半圆,要用这个半圆做一个圆锥的侧面和底面,小芳想这样做:在圆弧上取点C,使∠AOC=60°,用扇形OBC作圆锥的侧面,在扇形OAC内剪一个最大的⊙M作圆锥的底面,你认为小芳这样做办得到吗?请你通过计算说明理由.
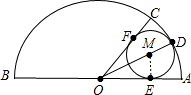 解:连接OE.
解:连接OE.∵⊙M与OA相切于E,
∴ME⊥OA,
设⊙M的半径为r,
∵OC切圆O于F,OA切圆O于E,
∴OD平分∠AOC,
∴∠MOE=
 ∠AOC=30°
∠AOC=30°∴OM=2r
∵2r+r=R∴r=
 R,
R,∴⊙M的周长
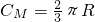
而弧BC=
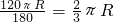 ,
,∴小芳这样办得到.
分析:连接OE,利用⊙M与OA相切于E得到ME⊥OA,然后设⊙M的半径为r,利用两圆之间的关系表示出⊙M的周长,从而求得弧BC的长,然后即可做出判断.
点评:本题考查了圆锥的计算,解题的关键是利用两圆的关系求得⊙M的周长,进而求得弧BC的长.

练习册系列答案
相关题目
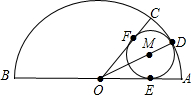 如图:有一个半径为R的半圆,要用这个半圆做一个圆锥的侧面和底面,小芳想这样做:在圆弧上取点C,使∠AOC=60°,用扇形OBC作圆锥的侧面,在扇形OAC内剪一个最大的⊙M作圆锥的底面,你认为小芳这样做办得到吗?请你通过计算说明理由.
如图:有一个半径为R的半圆,要用这个半圆做一个圆锥的侧面和底面,小芳想这样做:在圆弧上取点C,使∠AOC=60°,用扇形OBC作圆锥的侧面,在扇形OAC内剪一个最大的⊙M作圆锥的底面,你认为小芳这样做办得到吗?请你通过计算说明理由.
 如图,有一个半径为50米的圆形草坪,现在沿草坪的四周开辟了宽10米的环形跑道,那么:
如图,有一个半径为50米的圆形草坪,现在沿草坪的四周开辟了宽10米的环形跑道,那么: