题目内容
(本小题10分)
抛物线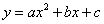 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).
(1)求该抛物线的解析式;
(2)画出此抛物线的草图;
(3)求证:△AOB是等腰直角三角形;
(4)将△AOB绕点O按顺时针方向旋转135°得△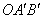 ,写出边
,写出边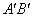 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
【答案】
(1)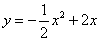
(2)图略
(3)证明略
(4)点P不在此抛物线上
【解析】解:(1)由题意可得
 ……2分
……2分
解得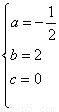
∴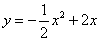 .……3分
.……3分
(2)如图.……5分

(3)如图,直线BC为抛物线的对称轴,
∴BC⊥x轴于点C,
在Rt△BOC中:OC=BC=2,∴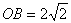 .
.
同理可得,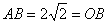 .
.
∵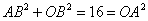 ,
,
∴△OAB为等腰直角三角形.……7分
(4)旋转135°后点 落在y轴上,如图,
落在y轴上,如图,
则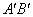 ⊥x轴,∴
⊥x轴,∴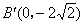 ,
,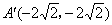 ……8分
……8分
∵点P为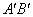 的中点,
的中点,
∴点P坐标为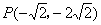 .……9分
.……9分
当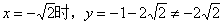 ,
,
∴点P不在此抛物线上.……10分

练习册系列答案
相关题目
 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2). ,写出边
,写出边 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由. 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).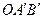 ,写出边
,写出边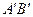 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.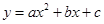 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).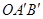 ,写出边
,写出边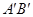 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.