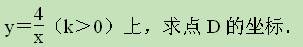题目内容
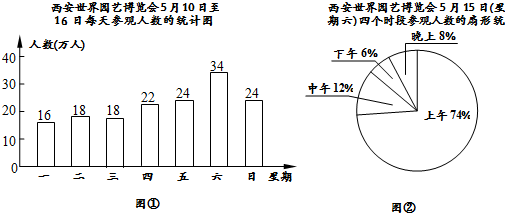
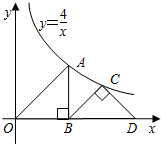
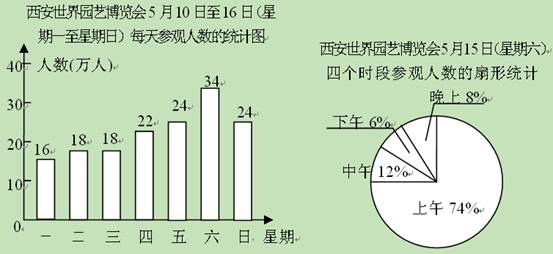
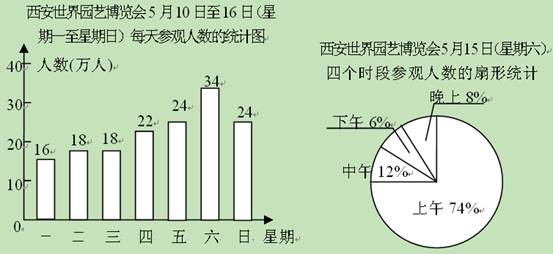
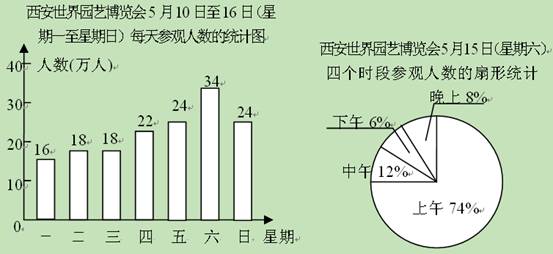
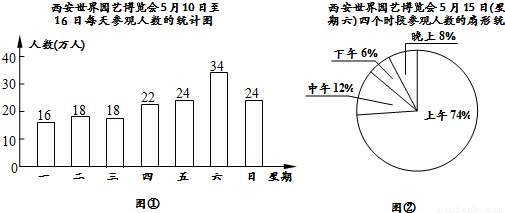
Ⅰ.爱养花的李先生为选择一个合适的时间去参观2011年西安世界园艺博览会,他查阅了5月10日至16日是(星期一至星期日)每天的参观人数,得到图(1)、图(2)所示的统计图.其中图(1)是每天参观人数的统计图,图(2)是5月15日是(星期六)这一天上午、中午、下午和晚上四个时段参观人数的扇形统计图,请你根据统计图解答下面的问题:(1)5月10日至16日这一周中,参观人数最多的是日是______,有______万人,参观人数最少的是日是______,有______万人,中位数是______.
(2)5月15日是(星期六)这一天,上午的参观人数比下午的参观人数多多少人?(精确到1万人)
(3)如果李先生想尽可能选择参观人数较少的时间参观世园会,你认为选择什么时间较合适?
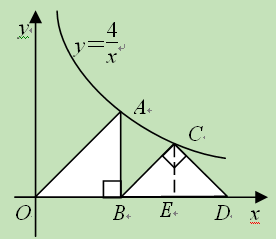
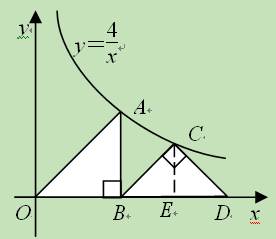
Ⅱ.如图在等腰Rt△OBA和Rt△BCD中,∠OBA=∠BCD=90°,点A和点C都在双曲线y=
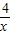 (k>0)上,求点D的坐标.
(k>0)上,求点D的坐标.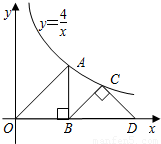
【答案】分析:Ⅰ.(1)看统计图即可得到答案;
(2)用上午的参观人数-下午的参观人数即可;
(3)根据图(2)知,下午或晚上参观人数较少.
Ⅱ.过C点作CE⊥BD于E,根据等腰直角三角形的性质得到OB=AB,即可求出A(2,2),得OB=2,又三角形CBD为等腰Rt,∠BCD=90°,得到CE=BE=DE,设CE=b,则OE=b+2,OD=2+2b,则C点坐标为(b+2,b),把它代入双曲线y= (k>0)求出b,即可得到OD,从而得点D的坐标.
(k>0)求出b,即可得到OD,从而得点D的坐标.
解答:解:Ⅰ.(1)答案为星期六;34;星期一;16;22;
(2)上午的参观人数-下午的参观人数=34×(74%-6%)≈23(万),
所以5月15日是(星期六)这一天,上午的参观人数比下午的参观人数多23万人;
(3)由图(2)知,下午或晚上参观人数较少,所以如果李先生想尽可能选择参观人数较少的时间参观世园会,选择下午或晚上参观较合适.
Ⅱ.过C点作CE⊥BD于E,如图,
∵△OBA为等腰Rt△,∠OBA=90°,
∴OB=AB,
设A(a,a),
∴a•a=4,
∴a=2,或a=-2(舍去),即OB=2,
又∵△CBD为等腰Rt△,∠BCD=90°,
∴CE=BE=DE,
设CE=b,则OE=b+2,OD=2+2b,
∴C点坐标为(b+2,b),
∴(b+2)•b=4,解得b= -1,或b=-
-1,或b=- -1(舍去),
-1(舍去),
∴OD=2 ,
,
∴点D的坐标为(2 ,0).
,0).
点评:本题考查了解反比例函数综合题的方法:通过反比例的解析式和几何条件确定点的坐标.也考查了观察统计图的能力和中位数的概念.
(2)用上午的参观人数-下午的参观人数即可;
(3)根据图(2)知,下午或晚上参观人数较少.
Ⅱ.过C点作CE⊥BD于E,根据等腰直角三角形的性质得到OB=AB,即可求出A(2,2),得OB=2,又三角形CBD为等腰Rt,∠BCD=90°,得到CE=BE=DE,设CE=b,则OE=b+2,OD=2+2b,则C点坐标为(b+2,b),把它代入双曲线y=
 (k>0)求出b,即可得到OD,从而得点D的坐标.
(k>0)求出b,即可得到OD,从而得点D的坐标.解答:解:Ⅰ.(1)答案为星期六;34;星期一;16;22;
(2)上午的参观人数-下午的参观人数=34×(74%-6%)≈23(万),
所以5月15日是(星期六)这一天,上午的参观人数比下午的参观人数多23万人;
(3)由图(2)知,下午或晚上参观人数较少,所以如果李先生想尽可能选择参观人数较少的时间参观世园会,选择下午或晚上参观较合适.
Ⅱ.过C点作CE⊥BD于E,如图,

∵△OBA为等腰Rt△,∠OBA=90°,
∴OB=AB,
设A(a,a),
∴a•a=4,
∴a=2,或a=-2(舍去),即OB=2,
又∵△CBD为等腰Rt△,∠BCD=90°,
∴CE=BE=DE,
设CE=b,则OE=b+2,OD=2+2b,
∴C点坐标为(b+2,b),
∴(b+2)•b=4,解得b=
 -1,或b=-
-1,或b=- -1(舍去),
-1(舍去),∴OD=2
 ,
,∴点D的坐标为(2
 ,0).
,0).点评:本题考查了解反比例函数综合题的方法:通过反比例的解析式和几何条件确定点的坐标.也考查了观察统计图的能力和中位数的概念.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目