题目内容
如图,周长为10的矩形OABC(OC<OA)在直角坐标系中,其中一个顶点B恰在函数y=| 4 | x |
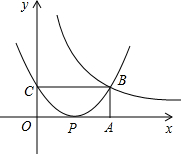 x>0)的图象上.
x>0)的图象上.(1)矩形OABC的面积为
(2)是确定A,B,C三点的坐标;
(3)若抛物线y=ax2+bx+c经过B,C两点,且顶点P在x轴上,试确定其解析式.
分析:(1)由点B在双曲线上,则矩形OABC的面积为点B横纵坐标乘积的绝对值;
(2)设矩形的宽AB=x,则矩形的长(5-x),根据矩形的面积可得出x,从而得出A,B,C三点的坐标;
(3)根据题意可得出抛物线的顶点的坐标,可设抛物线的解析式为y=a(x-2)2,将点C代入即可得出a,即可求得二次函数的解析式.
(2)设矩形的宽AB=x,则矩形的长(5-x),根据矩形的面积可得出x,从而得出A,B,C三点的坐标;
(3)根据题意可得出抛物线的顶点的坐标,可设抛物线的解析式为y=a(x-2)2,将点C代入即可得出a,即可求得二次函数的解析式.
解答:解:(1)矩形OABC的面积为4;
(2)设矩形的宽AB=x,则矩形的长(5-x),
∵矩形的OABC的面积为4,
∴x(5-x)=4,
解得x=1或4(不合题意,舍去)
即矩形的长为4,宽为1,
∴A(4,0),B(4,1),C(0,1).
(3)∵抛物线y=ax2+bx+c经过B、C两点,且顶点P在x轴上,
由抛物线的对称性可知其顶点为(2,0),
∴抛物线的解析式可设为y=a(x-2)2,
由抛物线经过点C(0,1),
∴1=a(x-2)2,解得a=
,
∴抛物线的解析式为y=
(x-2)2.
(2)设矩形的宽AB=x,则矩形的长(5-x),
∵矩形的OABC的面积为4,
∴x(5-x)=4,
解得x=1或4(不合题意,舍去)
即矩形的长为4,宽为1,
∴A(4,0),B(4,1),C(0,1).
(3)∵抛物线y=ax2+bx+c经过B、C两点,且顶点P在x轴上,
由抛物线的对称性可知其顶点为(2,0),
∴抛物线的解析式可设为y=a(x-2)2,
由抛物线经过点C(0,1),
∴1=a(x-2)2,解得a=
| 1 |
| 4 |
∴抛物线的解析式为y=
| 1 |
| 4 |
点评:本题是一道二次函数的综合题,考查了矩形的面积,用待定系数法求二次函数的解析式,此题难度不大.

练习册系列答案
相关题目
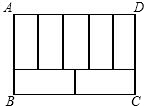 如图,周长为68的矩形ABCD被分成7个形状大小一样的矩形,则矩形ABCD的面积是
如图,周长为68的矩形ABCD被分成7个形状大小一样的矩形,则矩形ABCD的面积是 如图,周长为34的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为
如图,周长为34的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为 (
( x>0)的图象上.
x>0)的图象上. (x>0)的图象上.
(x>0)的图象上.