题目内容
(1)解不等式组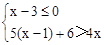 并把解集在数轴上表示出来;
并把解集在数轴上表示出来;

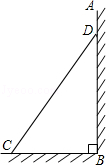
(2)如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
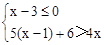 并把解集在数轴上表示出来;
并把解集在数轴上表示出来;
(2)如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

(1)解: 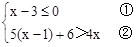 ,
,
解不等式①得:x≤3,
解不等式②得,x>﹣1,
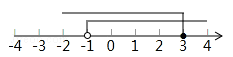
则不等式的解集为:﹣1<x≤3。
不等式组的解集在数轴上表示为:
(2)解:在Rt△BCD中,
∵∠DBC=90°,∠BCD=55°,CD=6米,
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92(米)。
∴AD=AB﹣BD≈6.5﹣4.92=1.58≈1.6(米)。
答:梯子的顶端与墙顶的距离AD为1.6米
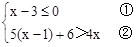 ,
,解不等式①得:x≤3,
解不等式②得,x>﹣1,
则不等式的解集为:﹣1<x≤3。
不等式组的解集在数轴上表示为:

(2)解:在Rt△BCD中,
∵∠DBC=90°,∠BCD=55°,CD=6米,
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92(米)。
∴AD=AB﹣BD≈6.5﹣4.92=1.58≈1.6(米)。
答:梯子的顶端与墙顶的距离AD为1.6米
试题分析:(1)解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解)。
不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个。在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示。
(2)在Rt△BCD中,根据∠BCD=55°,CD=6米,解直角三角形求出BD的长度,继而可求得AD=AB﹣BD的长度。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 的不等式
的不等式 ,下列说法正确的是( )
,下列说法正确的是( )

 取何值,不等式肯定有解
取何值,不等式肯定有解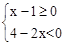 的最小整数解是 .
的最小整数解是 .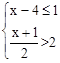 的解集是 .
的解集是 .
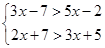 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.