题目内容
【题目】解下列方程组和不等式组
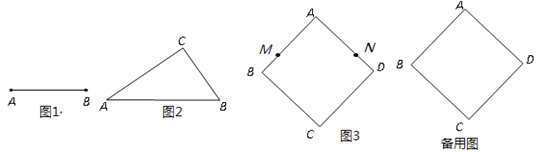
（1）
（2）
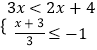（并把解集在数轴上表示出来）
【答案】
（1）解：②×4得：4x﹣4y=16 ③
①+③得：7x=35
x=5
将x=5代入②中得：5﹣y=4
y=1
则方程组的解是 
（2）解：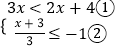 
，
解①得x＜4，
解②得x≥3．
则不等式组的解集是：3≤x＜4．
【解析】（1）利用加减法即可求解；（2）首先解每个不等式．两个不等式的解集的公共部分就是不等式组的解集．
【考点精析】本题主要考查了解二元一次方程组和不等式的解集在数轴上的表示的相关知识点，需要掌握二元一次方程组：①代入消元法；②加减消元法；不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈才能正确解答此题．
练习册系列答案
相关题目
【题目】雅安地震发生后，全国人民抗震救灾，众志成城，值地震发生一周年之际，某地政府又筹集了重建家园的必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型 | 甲 | 乙 | 丙 |
汽车运载量（吨/辆） | 5 | 8 | 10 |
汽车运费（元/辆） | 400 | 500 | 600 |
（1）全部物资可用甲型车8辆，乙型车5辆，丙型车 辆来运送．
（2）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（3）为了节省运费，该地政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为14辆，你能分别求出三种车型的辆数吗？此时的运费又是多少元？
