题目内容
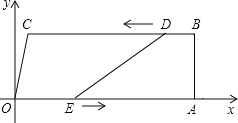
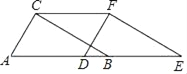
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的面积.
【答案】(1)3cm(2)![]()
【解析】试题分析:(1)根据勾股定理求出AB=![]() =5cm.利用平移的性质可得AB=DE=5cm,然后根据AD=AE-DE求解即可;
=5cm.利用平移的性质可得AB=DE=5cm,然后根据AD=AE-DE求解即可;
(2)作CG⊥AB于G,根据三角形的面积公式求出CG,根据梯形的面积公式求出四边形AEFC的面积即可.
试题解析:
(1)∵在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
∴AB=![]() =5cm.
=5cm.
∵△ABC沿AB方向向右平移得到△DEF,
∴AD=BE=CF,BC=EF=3cm,AB=DE=5cm.
∵AE=8cm,
∴AD=AE﹣DE=3cm;
(2)作CG⊥AB于G,如图,
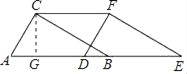
由三角形的面积公式得:CGAB=ACBC,
∴5×CG=3×4,
∴CG=![]() ,
,
∴四边形AEFC的面积=![]() (CF+AE)×CG=
(CF+AE)×CG=![]() ×(3+8)×
×(3+8)×![]() =
=![]() .
.
答:四边形AEFC的面积是![]() cm2.
cm2.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目