题目内容
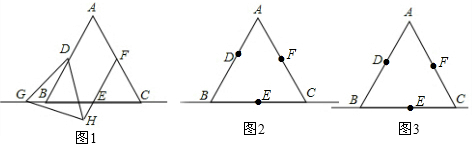
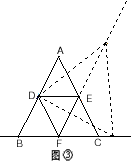
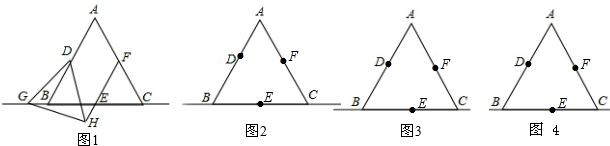
已知:在等边△ABC中,点D、E、F分别为边AB、BC、AC的中点,点G为直线BC上一动点,当点G在CB延长线上时,有结论“在直线EF上存在一点H,使得△DGH是等边三角形”成立(如图①),且当点G与点B、E、C重合时,该结论也一定成立。问题:当点G在直线BC的其它位置时,该结论是否仍然成立?请你在下面的备用图②③④中,画出相应图形并证明相关结论。
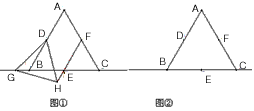
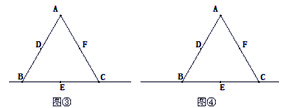
| 证明:连接DE、EF、DF; (1)当点G在线段BE上时,如图①, 在EF上截取EH使EH=BG, ∵D、E、F是等边△ABC三边中点, ∴△DEF、△DBE也是等边三角形且DE=AB=  BD BD在△DBG和△DEH中, 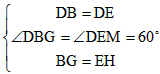 , ,∴△DBG≌△DEH, ∴DG=DH, ∴∠BDG=∠EDH, ∵∠BDE=∠GDE+∠BDG=60°, ∴∠GDH=∠GDE+∠EDH=60°, ∴在直线EF上存在点H使得△DGH是等边三角形; (2)当点G在射线EC上时,如图②,在EF上截取EH使EH=BG, 由(1)可证△DBG≌△DEH, ∴DG=DH,∠BDG=∠EDH, ∵∠BDE=∠BDG-∠EDG=60°, ∴∠GDH=∠EDH-∠EDG=60°, ∴在直线EF上存在点H使得△DGH是等边三角形; (3)当点G在BC延长线上时,如图③, 与(2)同理可证,结论成立; 综上所述,点G在直线BC上的任意位置时,该结论成立。 |
   |

练习册系列答案
相关题目
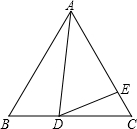 已知:在等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:在等边△ABC中,AB、cosB是关于x的方程x2-4mx-