Question

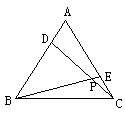
如图，已知：在等边△ABC中，D、E分别在AB、AC上，且AD=CE，BE、CD相交于点P．

（1）说明△ADC≌△CEB的理由；

（2）求∠BPC的度数．

 

Answer 1

【答案】

（1）证明：∵△ABC为等边三角形，

∴AB=BC=AC，∠A=∠ABC=∠ACB=60°，

在△ADC和△CEB中，

，

∴△ADC≌△CEB（SAS）；；

 

（2）解：∵△ADC≌△CEB，

∴∠ACD=∠CBE，

又∵∠ACB=∠ACD+∠DCB=60°，

∴∠CBE+∠DCB=60°，

∴∠BPC=120°．

【解析】（1）由三角形ABC为等边三角形，根据等边三角形的性质可知三边相等，三内角都为60°，可得AC=CB，∠A=∠ACB=60°，又AD=CE，利用SAS的方法可得三角形ADC与三角形CEB全等；

（2）由（1）证明的两三角形全等，根据全等三角形的对应角相等可得∠ACD=∠CBE，又∠ACB=∠ACD+∠DCB=60°，等量代换可得∠CBE+∠DCB=60°，最后利用三角形的内角和定理即可求出∠BPC的度数．