题目内容
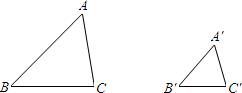 图中的两个三角形相似,且AB=2,A′B′=1,则△ABC与△A′B′C′的相似比是
图中的两个三角形相似,且AB=2,A′B′=1,则△ABC与△A′B′C′的相似比是
- A.1:2
- B.2:1
- C.3:1
- D.1:3
B
分析:由两个三角形相似,且AB=2,A′B′=1,根据相似比等于相似三角形对应边的比,即可求得答案.
解答:∵△ABC∽△A′B′C′,且AB=2,A′B′=1,
∴△ABC与△A′B′C′的相似比是:AB:A′B′=2:1.
故选B.
点评:此题考查了相似三角形的性质.此题比较简单,注意掌握相似比的定义.
分析:由两个三角形相似,且AB=2,A′B′=1,根据相似比等于相似三角形对应边的比,即可求得答案.
解答:∵△ABC∽△A′B′C′,且AB=2,A′B′=1,
∴△ABC与△A′B′C′的相似比是:AB:A′B′=2:1.
故选B.
点评:此题考查了相似三角形的性质.此题比较简单,注意掌握相似比的定义.

练习册系列答案
相关题目
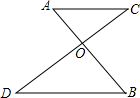 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= 图中的两个三角形相似,且AB=2,A′B′=1,则△ABC与△A′B′C′的相似比是( )
图中的两个三角形相似,且AB=2,A′B′=1,则△ABC与△A′B′C′的相似比是( )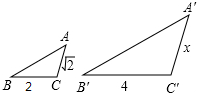
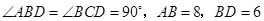 ,当
,当 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.
