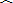Question

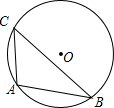
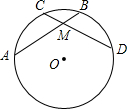
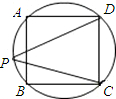
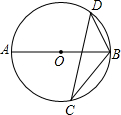
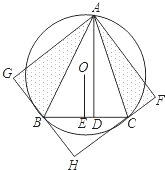
如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC，OE=

1

2

BC．将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．
①∠BAC=45°；
②四边形AFHG是正方形；
③BC=BG+CF；
④若BD=6，CD=4，则AD=10．
以上说法正确的有（　　）

A．4个

B．3个

C．2个

D．1个

Answer 1

连接OB和OC；
∵OE⊥BC，
∴BE=CE；
∵OE=

1

2

BC，
∴∠BOC=90°，
∴∠BAC=45°，选项①正确；
∵AD⊥BC，
∴∠ADB=∠ADC=90°；
由折叠可知，AG=AF=AD，∠AGH=∠AFH=90°，
∠BAG=∠BAD，∠CAF=∠CAD，
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°；
∴∠GAF=∠BAG+∠CAF+∠BAC=90°；
∴四边形AFHG是正方形，选项②正确；
由折叠可得：BD=BG，CD=CF，
∴BC=BD+CD=BG+CF，选项③正确，
由②得，∠BHC=90°，GH=HF=AD，GB=BD=6，CF=CD=4；
设AD的长为x，则BH=GH-GB=x-6，CH=HF-CF=x-4．
在Rt△BCH中，BH²+CH²=BC²，
∴（x-6）²+（x-4）²=10²；
解得，x₁=12，x₂=-2（不合题意，舍去）；
∴AD=12．选项④错误，
则正确的选项有3个．
故选B