Question

【题目】如图，直角梯形ABCD中，∠ADC＝90°，AD∥BC，点E在BC上，点F在AC上，∠DFC＝∠AEB．

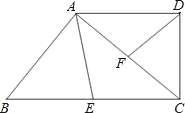
（1）求证：△ADF∽△CAE；

（2）当AD＝8，DC＝6，点E、F分别是BC、AC的中点时，求BC的长？

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）由题意可得∠DAC=∠ACE，∠AFD=∠AEC，即可证△ADF∽△CAE；

（2）由勾股定理可求AC=10，由△ADF∽△CAE可得，即可求EC的长度，即可求BC的长度.

证明：（1）∵AD∥BC,

∴∠DAC＝∠ACE,

∵∠DFC＝∠AEB,

∴∠AFD＝∠AEC且∠DAC＝∠ACE,

∴△ADF∽△CAE;

（2）∵AD＝8，DC＝6，∠ADC＝90°,

∴AC＝＝10,

∵点F是AC中点,

∴AF＝5

∵△ADF∽△CAE,

∴,

即,

∴CE＝,

∵点E是BC中点,

∴BC＝2CE＝.