在正方形网格中建立如图所示的坐标系.每个小正方形的边长都为1.网格中有一个格点△ABC(即三角形的顶点都在格点上)．(1)在图中作出△ABC关于y轴对称的△A1B1C1.并直接写出点A1的坐标(要求:A与A1.B与B1.C与C1相对应),题的结果下.连接AA1.BB1.求四边形AA1B1B的面积．题目和参考答案——青夏教育精英家教网—

题目内容

在正方形网格中建立如图所示的坐标系，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
（1）在图中作出△ABC关于y轴对称的△A₁B₁C₁，并直接写出点A₁的坐标（要求：A与A₁，B与B₁，C与C₁相对应）；
（2）在第（1）题的结果下，连接AA₁，BB₁，求四边形AA₁B₁B的面积．

分析：（1）根据A、B、C的坐标可得到关于y轴对称的坐标，再描出点，连接即可；
（2）根据图形可得四边形AA₁B₁B是等腰梯形，利用梯形面积公式进行计算即可．

解答：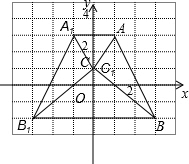

解：（1）如图，△A₁B₁C₁就是所求画的三角形，
点A₁的坐标为（-1，3）；

（2）由画图可知：四边形AA₁B₁B为等腰梯形，其中，AA₁=2，BB₁=6，高为5．
S_梯形AA1B1B=

（2+6）×5=20．

点评：此题主要考查了画轴对称图形，以及求四边形的面积，关键是掌握关于y轴对称的点的坐标特点：横坐标是互为相反数，纵坐标不变．

练习册系列答案

相关题目

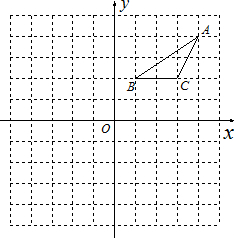21、在正方形网格中建立如图所示的平面直角坐标系xoy．△ABC的三个顶点都在格点上，点A的坐标是（4，4 ），请解答下列问题：
（1）将△ABC向下平移5个单位长度，画出平移后的A₁B₁C₁，并写出点A的对应点A₁的坐标；
（2）画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；
（3）将△ABC绕点C逆时针旋转90°，画出旋转后的的△A₃B₃C．

24、在正方形网格中建立如图所示的直角坐标系，设网格中小正方形的边长是单位长度1，已知网格中⊙A的半径是4，点A（-7，-2），点C（3，0）按下列要求在网格中画图并回答问题：
（1）将⊙A先向上平移8个单位，再向右平移4个单位得⊙B，画出⊙B；
（2）画出⊙D，使⊙D与⊙B关于点C成位似，位似比为1：2，并判断点D与⊙B的位置关系是

点D在⊙B上或⊙B外

．

在正方形网格中建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请回答下列问题：
（1）将△ABC向下平移五个单位长度，画出平移后的△A₁B₁C₁并写出点A的对应点A₁的坐标；
（2）画出△ABC关于原点O对称的△A₂B₂C₂，并写出△A₂B₂C₂各顶点坐标；
（3）求出点A旋转到A₂的路程是多少？

（2011•海南）在正方形网格中建立如图所示的平面直角坐标系xoy．△ABC的三个顶点都在格点上，点A的坐标是（4，4 ），请解答下列问题；
（1）将△ABC向下平移5个单位长度，画出平移后的A₁B₁C₁，并写出点A的对应点A₁的坐标；
（2）画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；
（3）将△ABC绕点C逆时针旋转90°，画出旋转后的的△A₃B₃C．

试题分类