题目内容
 24、在正方形网格中建立如图所示的直角坐标系,设网格中小正方形的边长是单位长度1,已知网格中⊙A的半径是4,点A(-7,-2),点C(3,0)按下列要求在网格中画图并回答问题:
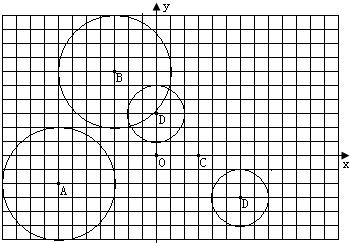
24、在正方形网格中建立如图所示的直角坐标系,设网格中小正方形的边长是单位长度1,已知网格中⊙A的半径是4,点A(-7,-2),点C(3,0)按下列要求在网格中画图并回答问题:(1)将⊙A先向上平移8个单位,再向右平移4个单位得⊙B,画出⊙B;
(2)画出⊙D,使⊙D与⊙B关于点C成位似,位似比为1:2,并判断点D与⊙B的位置关系是
点D在⊙B上或⊙B外
.分析:(1)把圆心A先向上平移8个单位,再向右平移4个单位得点B,以点B为圆心,4为半径画圆即可;
(2)延长BC到D,使CD等于BC的一半,或连接BC,找到BC的中点D,然后以点D为圆心,以2为半径画圆即可得到⊙D,也就得到了点D相对于⊙B的位置.
(2)延长BC到D,使CD等于BC的一半,或连接BC,找到BC的中点D,然后以点D为圆心,以2为半径画圆即可得到⊙D,也就得到了点D相对于⊙B的位置.
解答:解:(1)画出⊙B(2分)
(2)画出⊙D(两个图各1分)(4分)
点D在⊙B外(6分)
(2)画出⊙D(两个图各1分)(4分)
点D在⊙B外(6分)

点评:圆的平移的关键是找准圆心;注意跟⊙B位似比为1:2的圆有2个.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
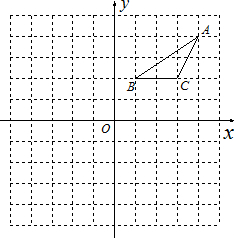 21、在正方形网格中建立如图所示的平面直角坐标系xoy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题:
21、在正方形网格中建立如图所示的平面直角坐标系xoy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题: 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请回答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请回答下列问题: 在正方形网格中建立如图所示的坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
在正方形网格中建立如图所示的坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上). 的A1B1C1,并写出点A的对应点A1的坐标;
的A1B1C1,并写出点A的对应点A1的坐标;