题目内容
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.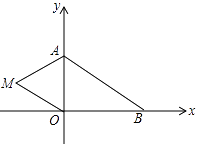
(1)a= , b=;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣ ![]() 时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
【答案】
(1)2,3
(2)解:∵在第二象限内有一点M(m,1),
∴S△AMO= ![]() ×AO×(﹣m)=﹣m,
×AO×(﹣m)=﹣m,
S△AOB= ![]() ×AO×OB=3,
×AO×OB=3,
∴四边形ABOM的面积为:3﹣m;
(3)解:∵当m=﹣ ![]() 时,△ABN的面积与四边形ABOM的面积相等,
时,△ABN的面积与四边形ABOM的面积相等,
当N在x轴的负半轴时,设N点坐标为:(c,0),
则 ![]() ×2(3﹣c)=3﹣(﹣
×2(3﹣c)=3﹣(﹣ ![]() ),
),
解得:c=﹣1.5,
故N(﹣1.5,0),
当N在y轴的负半轴时,设N点坐标为:(0,d),
则 ![]() ×3(2﹣d)=3﹣(﹣
×3(2﹣d)=3﹣(﹣ ![]() ),
),
解得:d=﹣1,
故N(0,﹣1),
综上所述:N点坐标为:(﹣1.5,0),(0,﹣1).
【解析】解:(1)∵|a﹣2|+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
解得:a=2,b=3,
所以答案是:2,3;

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目