题目内容
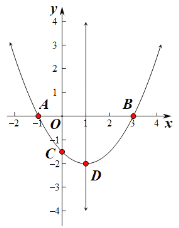
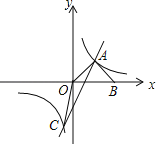
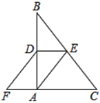
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为( )
A.8B.9C.10D.11
【答案】A
【解析】
根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.
解:在Rt△ABC中,∵AC=3,AB=4,
∴BC=5,
∵E是BC的中点,
∴AE=BE=2.5,
∴∠BAE=∠B,
∵∠FDA=∠B,
∴∠FDA=∠BAE,
∴DF∥AE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=![]() AC=1.5,
AC=1.5,
∴四边形AEDF是平行四边形,
∴四边形AEDF的周长=2×(1.5+2.5)=8.
故选:A.

【题目】我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量![]() (万件与月份
(万件与月份![]() (月)的关系为:
(月)的关系为: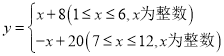
每件产品的利润![]() (元)与月份
(元)与月份![]() (月)的关系如下表:
(月)的关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() 请你根据表格直接写出每件产品利润z (元) 与月份
请你根据表格直接写出每件产品利润z (元) 与月份![]() (月)的函数关系式;
(月)的函数关系式;
![]() 若月利润
若月利润![]() (万元) =当月销售量
(万元) =当月销售量![]() (万件)
(万件) ![]() 当月每件产品的利润
当月每件产品的利润![]() (元),求月利润
(元),求月利润![]() (万元)与月份
(万元)与月份![]() (月)的关系式;
(月)的关系式;
![]() 当
当![]() 为何值时,月利润
为何值时,月利润![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
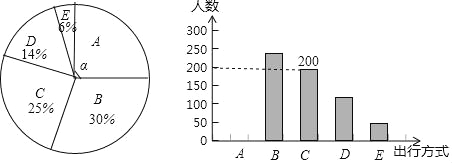
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.