题目内容
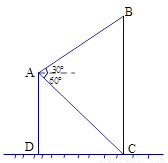
如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为12m．求旗杆的高度．
分析：过A作AE⊥BC于E，在Rt△ACE中，已知了CE的长，可利用俯角∠CAE的正切函数求出AE的值；进而在Rt△ABE中，利用仰角∠BAE的正切函数求出BE的长；BC=BE+CE．
解答：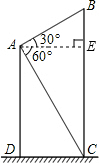
解：过A作AE⊥BC于E．
∵AD∥CE，
∴Rt△ACE中，CE=AD=12m，∠CAE=60°，
∴AE=CE÷tan60°=4
．
Rt△AEB中，AE=4
，∠BAE=30°，
∴BE=AE•tan30°=4．
BC=BE+CE=4+12=16．
故旗杆的高度为16米．
解：过A作AE⊥BC于E．∵AD∥CE，
∴Rt△ACE中，CE=AD=12m，∠CAE=60°，
∴AE=CE÷tan60°=4
| 3 |
Rt△AEB中，AE=4
| 3 |
∴BE=AE•tan30°=4．
BC=BE+CE=4+12=16．
故旗杆的高度为16米．
点评：本题考查直角三角形的解法，首先构造直角三角形，再运用三角函数的定义解题．
练习册系列答案
相关题目
（2013•贺州）如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25°，测得大树底部C的俯角为45°．已知点A距地面的高度AD为12m，求大树的高度BC．（最后结果精确到0.1）
