题目内容
（2013•贺州）如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25°，测得大树底部C的俯角为45°．已知点A距地面的高度AD为12m，求大树的高度BC．（最后结果精确到0.1）分析：过A作AE⊥BC于E，在Rt△ACE中，已知CE的长，可利用俯角∠CAE的正切函数求出AE的值；进而在Rt△ABE中，利用仰角∠BAE的正切函数求出BE的长；则BC=BE+CE．
解答：
解：过A作AE⊥BC于E，则四边形ADCE是矩形，CE=AD=12m．
在Rt△ACE中，∵∠EAC=45°，
∴AE=CE=12m，
在Rt△AEB中，∠BAE=25°，
∴BE=AE•tan25°≈12×0.47=5.64m．
∴BC=BE+CE≈5.64+12≈17.6．
答：大树的高度约为17.6m．
解：过A作AE⊥BC于E，则四边形ADCE是矩形，CE=AD=12m．在Rt△ACE中，∵∠EAC=45°，
∴AE=CE=12m，
在Rt△AEB中，∠BAE=25°，
∴BE=AE•tan25°≈12×0.47=5.64m．
∴BC=BE+CE≈5.64+12≈17.6．
答：大树的高度约为17.6m．
点评：此题考查了仰角与俯角的知识．此题难度适中，注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键．
练习册系列答案
相关题目
（2013•贺州）如图是一个几何体的三视图，根据图中提供的数据（单位：cm）可求得这个几何体的体积为（ ）
（2013•贺州）如图，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF的长是（ ）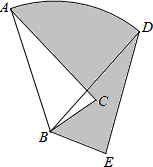
（2013•贺州）如图，在△ABC中，AB=6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是
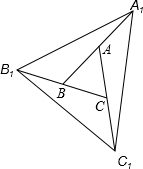（2013•贺州）如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积
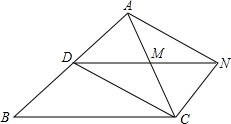（2013•贺州）如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．