ЬтФПФкШн
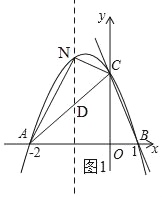
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓНЛxжсгкAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌНЛyжсгкCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгACЃЌдкжБЯпACЩЯЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуNЃЌЪЙЁїNACЕФУцЛ§зюДѓЃЌШєДцдкЃЌЧѓГіетИізюДѓжЕМАДЫЪБЕуNЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуMдкxжсЩЯЃЌЪЧЗёДцдкЕуMЃЌЪЙвдBЁЂCЁЂMЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌШєДцдкЃЌжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ4ЃЉШєPЮЊХзЮяЯпЩЯвЛЕуЃЌЙ§PзїPQЁЭBCгкQЃЌдкyжсзѓВрЕФХзЮяЯпЪЧЗёДцдкЕуPЪЙЁїCPQЁзЁїBCOЃЈЕуCгыЕуBЖдгІЃЉЃЌШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љx+2ЃЛЃЈ2ЃЉNЃЈЉ1ЃЌ2ЃЉЃЌЁїANCЕФУцЛ§газюДѓжЕЮЊ1ЃЛЃЈ3ЃЉMЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЛЃЈ4ЃЉЕуPЕФзјБъЮЊЃКЃЈЉ1ЃЌ2ЃЉЛђЃЈ
ЃЌ0ЃЉЃЛЃЈ4ЃЉЕуPЕФзјБъЮЊЃКЃЈЉ1ЃЌ2ЃЉЛђЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУНЛЕуЪНЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжБЯпACЕФНтЮіЪНЃЌзїИЈжњЯпNDЃЌИљОнХзЮяЯпЕФНтЮіЪНБэЪОNЕФзјБъЃЌИљОнжБЯпACЕФНтЮіЪНБэЪОDЕФзјБъЃЌБэЪОNDЕФГЄЃЌРћгУЧІжБИпЖШгыЫЎЦНПэЖШЕФЛ§ЧѓШ§НЧаЮANCЕФУцЛ§ЃЌИљОнЖўДЮКЏЪ§ЕФзюжЕПЩЕУУцЛ§ЕФзюДѓжЕЃЌВЂМЦЫуДЫЪБNЕФзјБъЃЛ
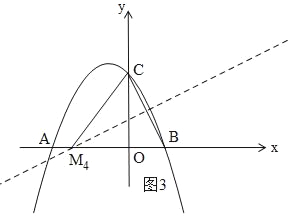
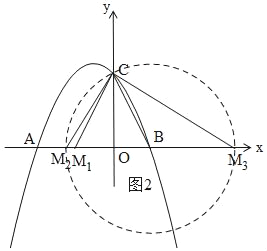
ЃЈ3ЃЉЗжШ§жжЧщПіЃКЕБBЁЂCЁЂMЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌЗжБ№вдШ§БпЮЊбќЃЌЛЭМаЮЃЌЧѓMЕФзјБъМДПЩЃЛ
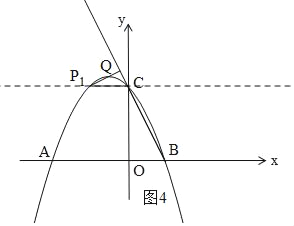
ЃЈ4ЃЉДцдкСНжжЧщПіЃКЂйШчЭМ4ЃЌЕуP1гыЕуCЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЪБЗћКЯЬѕМўЃЛ
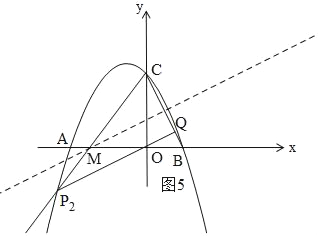
ЂкШчЭМ5ЃЌЭМ3жаЕФMЃЈЉ![]() ЃЌ0ЃЉЪБЃЌMB=MCЃЌЩшCMгыХзЮяЯпНЛгкЕуP2ЃЌдђЁїCP2QЁзЁїBCOЃЌP2ЮЊжБЯпCMЕФХзЮяЯпЕФНЛЕуЃЎ
ЃЌ0ЃЉЪБЃЌMB=MCЃЌЩшCMгыХзЮяЯпНЛгкЕуP2ЃЌдђЁїCP2QЁзЁїBCOЃЌP2ЮЊжБЯпCMЕФХзЮяЯпЕФНЛЕуЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉЁпЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓНЛxжсгкAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
ЩшЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃКy=aЃЈx+2ЃЉЃЈxЉ1ЃЉЃЌ
АбCЃЈ0ЃЌ2ЃЉДњШыЕУЃК2=aЃЈ0+2ЃЉЃЈ0Љ1ЃЉЃЌ
a=Љ1ЃЌ
Ёрy=ЉЃЈx+2ЃЉЃЈxЉ1ЃЉ=Љx2Љx+2ЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃКy=Љx2Љx+2.
ЃЈ2ЃЉШчЭМ1ЃЌЙ§NзїNDЁЮyжсЃЌНЛACгкDЃЌЩшNЃЈnЃЌЉn2Љn+2ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊЃКy=kx+bЃЌ
АбAЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ2ЃЉДњШыЕУЃК ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊЃКy=x+2ЃЌ
ЁрDЃЈnЃЌn+2ЃЉЃЌ
ЁрND=ЃЈЉn2Љn+2ЃЉЉЃЈn+2ЃЉ=Љn2Љ2nЃЌ
ЁрSЁїANC=![]() ЁС2ЁС[Љn2Љ2n]=Љn2Љ2n=ЉЃЈn+1ЃЉ2+1ЃЌ
ЁС2ЁС[Љn2Љ2n]=Љn2Љ2n=ЉЃЈn+1ЃЉ2+1ЃЌ
ЁрЕБn=Љ1ЪБЃЌЁїANCЕФУцЛ§газюДѓжЕЮЊ1ЃЌДЫЪБNЃЈЉ1ЃЌ2ЃЉЃЌ
ЃЈ3ЃЉДцдкЃЌЗжШ§жжЧщПіЃК
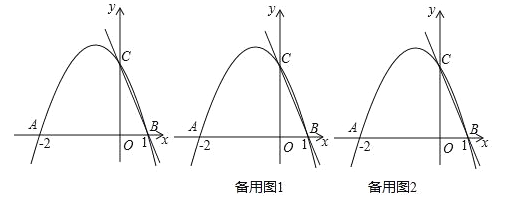
ЂйШчЭМ2ЃЌЕБBC=CM1ЪБЃЌM1ЃЈЉ1ЃЌ0ЃЉ.
ЂкШчЭМ2ЃЌгЩЙДЙЩЖЈРэЕУЃКBC=![]() =
=![]() ЃЌ
ЃЌ
вдBЮЊдВаФЃЌвдBCЮЊАыОЖЛдВЃЌНЛxжсгкM2ЁЂM3ЃЌдђBC=BM2=BM3=![]() ЃЌ
ЃЌ
ДЫЪБЃЌM2ЃЈ1Љ![]() ЃЌ0ЃЉЃЌM3ЃЈ1+
ЃЌ0ЃЉЃЌM3ЃЈ1+![]() ЃЌ0ЃЉ.
ЃЌ0ЃЉ.
ЂлШчЭМ3ЃЌзїBCЕФжаДЙЯпЃЌНЛxжсгкM4ЃЌСЌНгCM4ЃЌдђCM4=BM4ЃЌ
ЩшOM4=xЃЌдђCM4=BM4=x+1ЃЌ
гЩЙДЙЩЖЈРэЕУЃК22+x2=ЃЈ1+xЃЉ2ЃЌ
НтЕУЃКx=![]() ЃЌ
ЃЌ
ЁпM4дкxжсЕФИКАыжсЩЯЃЌ
ЁрM4ЃЈЉ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌЕБBЁЂCЁЂMЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌMЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЛђЃЈ1ЁР![]() ЃЌ0ЃЉЛђЃЈЉ
ЃЌ0ЃЉЛђЃЈЉ![]() ЃЌ0ЃЉ.
ЃЌ0ЃЉ.
ЃЈ4ЃЉДцдкСНжжЧщПіЃК
ЂйШчЭМ4ЃЌЙ§CзїxжсЕФЦНааЯпНЛХзЮяЯпгкP1ЃЌЙ§P1зїP1QЁЭBCЃЌ
ДЫЪБЃЌЁїCP1QЁзЁїBCOЃЌ
ЁрЕуP1гыЕуCЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЃЌ
ЁрP1ЃЈЉ1ЃЌ2ЃЉЃЌ
ЂкШчЭМ5ЃЌгЩЃЈ3ЃЉжЊЃКЕБMЃЈЉ![]() ЃЌ0ЃЉЪБЃЌMB=MCЃЌЩшCMгыХзЮяЯпНЛгкЕуP2ЃЌ
ЃЌ0ЃЉЪБЃЌMB=MCЃЌЩшCMгыХзЮяЯпНЛгкЕуP2ЃЌ
Й§P2зїP2QЁЭBCЃЌДЫЪБЃЌЁїCP2QЁзЁїBCOЃЌ
взЕУжБЯпCMЕФНтЮіЪНЮЊЃКy=![]() x+2ЃЌ
x+2ЃЌ
дђ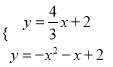 ЃЌ
ЃЌ
НтЕУЃКP2ЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃКЃЈЉ1ЃЌ2ЃЉЛђЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ