题目内容
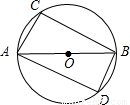
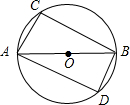 如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.
如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.
(1)求证:四边形ADBC是矩形;
(2)若∠ABC=30°,⊙O的半径是20厘米,求任意投掷一枚飞镖落在矩形区域内的概率.
证明:(1)∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°,
∵弦AC∥BD,
∴∠ABC=90°,
∴四边形ADBC是矩形;
(2)解:∵∠ABC=30°,⊙O的半径是20厘米,
∴AC=20,
BC=20 ,
,
矩形面积为:20×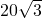 =400
=400 ,
,
圆的面积为:π×202=400π,
∴任意投掷一枚飞镖落在矩形区域内的概率为: =
= .
.
分析:(1)利用圆周角定理得出∠ACB=∠ADB=90°,再利用平行线的性质得出∠ABC=90°,即可得出答案;
(2)求出矩形面积以及圆的面积即可.
点评:此题主要考查了矩形的性质以及几何概率和圆周角定理,根据题意得出∠ACB=∠ADB=90°,∠ABC=90°是解决问题的关键.
∴∠ACB=∠ADB=90°,
∵弦AC∥BD,
∴∠ABC=90°,
∴四边形ADBC是矩形;
(2)解:∵∠ABC=30°,⊙O的半径是20厘米,
∴AC=20,
BC=20
 ,
,矩形面积为:20×
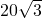 =400
=400 ,
,圆的面积为:π×202=400π,
∴任意投掷一枚飞镖落在矩形区域内的概率为:
 =
= .
.分析:(1)利用圆周角定理得出∠ACB=∠ADB=90°,再利用平行线的性质得出∠ABC=90°,即可得出答案;
(2)求出矩形面积以及圆的面积即可.
点评:此题主要考查了矩形的性质以及几何概率和圆周角定理,根据题意得出∠ACB=∠ADB=90°,∠ABC=90°是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
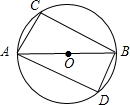 如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.
如图已知AB为⊙O的直径,弦AC∥BD,连接AD与BC.