题目内容
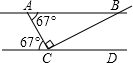（2010•郑州模拟）如图，AB∥CD，AC⊥BC，垂足为C，∠BAC=67?，则∠BCD=23
23
度．分析：由AB∥CD，∠BAC=67?，根据两直线平行，同旁内角互补，即可求得∠ACD的度数，又由AC⊥BC，根据垂直的定义，即可求得∠ACB的度数，继而可求得∠BCD的度数．
解答：解：∵AB∥CD，
∴∠ACD+∠BAC=180°，
∵∠BAC=67?，
∴∠ACD=113°，
∵AC⊥BC，
∴∠ACB=90°，
∴∠BCD=∠ACD-∠ACB=23°．
故答案为：23°．
∴∠ACD+∠BAC=180°，
∵∠BAC=67?，
∴∠ACD=113°，
∵AC⊥BC，
∴∠ACB=90°，
∴∠BCD=∠ACD-∠ACB=23°．
故答案为：23°．
点评：此题考查了平行线的性质与垂直的定义．此题比较简单，解题的关键是注意两直线平行，同旁内角互补定理的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
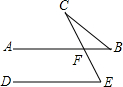（2010•郑州模拟）如图．AB∥DE，∠B+∠C=50°，则∠E=
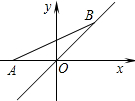（2010•郑州模拟）如图．点A的坐标为（-2.0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为