题目内容
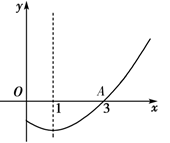
如图,已知抛物线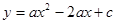 与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且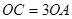 .点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作
.点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作 ,射线ET交线段OB于点F.
,射线ET交线段OB于点F.

(1) 求出此抛物线函数表达式,并直接写出直线BC的解析式;
(2)求证: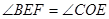 ;
;
(3)当 为等腰三角形时,求此时点E的坐标;
为等腰三角形时,求此时点E的坐标;
(4)点P为抛物线的对称轴与直线BC的交点,点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
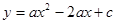 与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且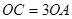 .点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作
.点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作 ,射线ET交线段OB于点F.
,射线ET交线段OB于点F.
(1) 求出此抛物线函数表达式,并直接写出直线BC的解析式;
(2)求证:
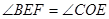 ;
;(3)当
 为等腰三角形时,求此时点E的坐标;
为等腰三角形时,求此时点E的坐标;(4)点P为抛物线的对称轴与直线BC的交点,点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)y=x2-x-3 (2)通过角的等量代换证明角相等(3)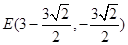 或者
或者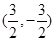
(4)M为
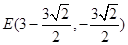 或者
或者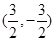
(4)M为

试题分析:解:(1)OC=3OA=3
∴C为(0,-3)
∵抛物线过(-1,0)和(0,-3)
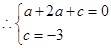
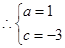
∴y=x2-x-3
BC:y=x-3
(2)∵OB=OC=3
∴∠OCB=∠OBC=45°
又∵∠OEF+∠BEF=∠COE+∠OCB
且∠OEF=45°
∴∠BEF=∠COE.
(3)①∵∠OFE=∠BEF+∠OBC>45°
∴∠OFE>∠OEF
∴OE>OF即OE≠OF.
②当OE=EF时,
∠BEF=∠COE,∠OCE=∠EBF
∴△COE≌△BEF(AAS)
∴BE=CO=3.
过E作ED ⊥x轴于D.
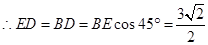
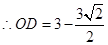
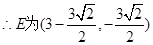
③当OF=EF时,则∠FOE=∠OEF=45°
∴∠OFE=90°.∴EF⊥OB.
∴E为BC的中点,∴E为
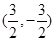 .
.(4)对称轴为x=1,
∴P为(1,-2).
①AP为边,
此时P点纵坐标为2或-2,
令x2-2x-3=2
即x2-2x-5=0
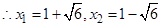
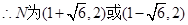
故

令x2-2x-3=-2
即x2-2x-1=0
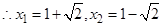
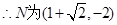 或
或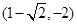
故
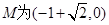 或
或
②AP为对角线,
设M为(x,0)
则N为(-x,-2)
∴x2+2x-3=-2
x2+2x-1=0
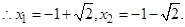

综上所述:M为
 .
.点评:该题较为复杂,主要考查学生对求二次函数解析式方法的掌握,以及在直角坐标系中分析函数与直线所都成几何图形点的坐标,需要考虑全面,分点论述。

练习册系列答案
相关题目
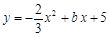 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
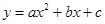 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①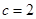 ;②
;②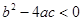 ;③当
;③当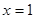 时,
时,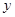 的最小值为
的最小值为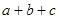 ,④
,④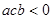 中,正确的有 .
中,正确的有 .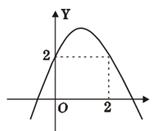
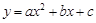 ,使它同时具有如下性质:
,使它同时具有如下性质: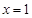 对称;②当x=2时,y>0;③当x=-2时,y<0.
对称;②当x=2时,y>0;③当x=-2时,y<0.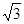 ,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒
,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒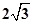 个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。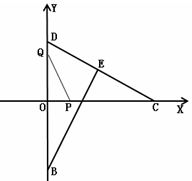
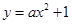 经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出:
经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出: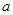 的取值范围为 ;
的取值范围为 ; 配方后为
配方后为 ,则
,则 的值分别为( )
的值分别为( ) ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(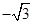 ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.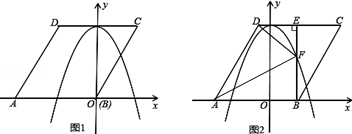
 图象的一部分,其对称轴为
图象的一部分,其对称轴为 ,若其与x轴一交点为A(3,0),则有图象可知不等式
,若其与x轴一交点为A(3,0),则有图象可知不等式 的解集是____________.
的解集是____________.