题目内容
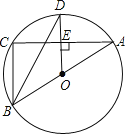
【题目】如图,平行四边形ABCD中,AD=9cm,CD=![]() cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)

(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
【答案】(1)3cm;(2)当t为![]() 时,四边形AMCN为菱形;(3)当t为4.5或1.5秒时,四边形MPNQ为正方形
时,四边形AMCN为菱形;(3)当t为4.5或1.5秒时,四边形MPNQ为正方形
【解析】
(1)先由平行四边形的性质得出AB=CD=3![]() cm.再解直角△ABE,即可求出AE的长度;
cm.再解直角△ABE,即可求出AE的长度;
(2)先证明四边形AMCN为平行四边形,则当AN=AM时,四边形AMCN为菱形.根据AN=AM列出方程32+(6-t)2=t2,解方程即可;
(3)先证明四边形MPNQ为矩形,则当QM=QN时,四边形MPNQ为正方形.根据QM=QN列出方程|2t-6|=3,解方程即可.
(1)∵四边形ABCD是平行四边形,
∴AB=CD=3![]() cm.
cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=ABsin∠B=3![]() ×
×![]() =3(cm);
=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=|6-t|,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=![]() .
.
所以当t为![]() 时,四边形AMCN为菱形;
时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=|t-(6-t)|=|2t-6|(注:分点Q在点M的左右两种情况),
∵QN=AE=3,
∴|2t-6|=3,
解得t=4.5或t=1.5.
所以当t为4.5或1.5秒时,四边形MPNQ为正方形.


【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调査分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 | 54 | 68 | 69 | 76 | 76 | 76 | 76 | 77 | 79 | 82 | 83 | 83 | 84 | 84 | 87 |
87 | 87 | 88 | 88 | 89 | 89 | 89 | 89 | 89 | 90 | 92 | 92 | 92 | 93 | 94 | |
乙校 | 57 | 61 | 63 | 71 | 72 | 73 | 76 | 79 | 80 | 83 | 84 | 84 | 84 | 85 | 85 |
87 | 87 | 88 | 89 | 89 | 90 | 90 | 91 | 92 | 92 | 92 | 92 | 92 | 94 | 94 |
(1)请根据乙校的数据补全条形统计图;

(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,请为他们各写出一条可以使用的理由;甲校: ;乙校; .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .