题目内容
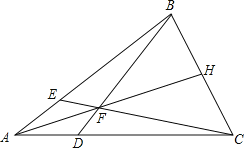
【题目】如图,△![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,
,![]() ∥
∥![]() ,
,![]() ,下列结论错误的是( )
,下列结论错误的是( )

A.![]() 30°B.
30°B.![]()
C.△![]() 的周长为10D.△
的周长为10D.△![]() 的周长为9
的周长为9
【答案】C
【解析】
根据等边三角形的性质和直角三角形两锐角互余的性质可判断A;
根据30°角的直角三角形的性质可判断B;
由B的结论结合![]() 为
为![]() 的中点可求出AB的长,进而可判断C;
的中点可求出AB的长,进而可判断C;
由![]() ∥
∥![]() 可判断△CEF是等边三角形,再求出CE的长即可判断D.
可判断△CEF是等边三角形,再求出CE的长即可判断D.
解:∵△![]() 是等边三角形,
是等边三角形,
∴AB=AC=BC,∠A=∠B=∠C=60°,
∵![]() ,∴∠AED=90°,
,∴∠AED=90°,
∴∠ADE=90°-∠A=30°,所以A正确;
∵AE=1,∠ADE=30°,∴AD=2AE=2,所以B正确;
∵![]() 为
为![]() 的中点,∴AB=2AD=4,∴△
的中点,∴AB=2AD=4,∴△![]() 的周长为4×3=12,所以C错误;
的周长为4×3=12,所以C错误;
∵![]() ∥
∥![]() ,
,
∴∠CEF=∠A=60°,∠CFE=∠B=60°,
∴△CEF是等边三角形,
∵AE=1,∴CE=AC-AE=3,
∴△![]() 的周长为9,所以D正确.
的周长为9,所以D正确.
故选C.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目