题目内容
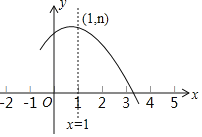
【题目】如图,已知一次函数y=![]() x-2与反比例函数y=
x-2与反比例函数y=![]() 的图象相交于点A(2, n) ,与x轴相交于点B.
的图象相交于点A(2, n) ,与x轴相交于点B.
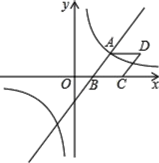
(1)求k 的值以及点 B 的坐标;
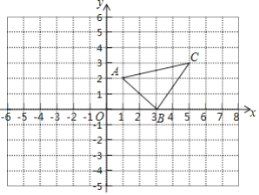
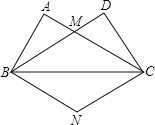
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)在y轴上是否存在点P,使PA+PB的值最小?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)k=6,点B的坐标为(![]() ,0);(2)D(2+
,0);(2)D(2+![]() ,3);(3)存在,P(0,
,3);(3)存在,P(0,![]() ).
).
【解析】
(1)把A点坐标代入一次函数解析式可求得n,则可求得A点坐标,代入反比例函数解析式则可求得k的值,最后根据y=0可得点B的坐标
(2)根据两点的距离公式可得AB的长,由菱形的边长相等可得AD=AB,根据AD与BC平行,可知A与D的纵坐标相等,由此可得D的坐标;
(3)作点B(![]() ,0)关于y轴的对称点Q的坐标为(
,0)关于y轴的对称点Q的坐标为(![]() ,0),连接AQ交y轴的交点为P,求出AQ解析式即可求解.
,0),连接AQ交y轴的交点为P,求出AQ解析式即可求解.
解:(1)把点A(2,n)代入一次函数y=![]() x2,
x2,
可得n=![]() ×22=3;
×22=3;
把点A(2,3)代入反比例函数y=![]() ,
,
可得k=xy=2×3=6,
∵一次函数y=![]() x2,与x轴相交于点B,
x2,与x轴相交于点B,
∴![]() x2=0,
x2=0,
解得x=![]() ,
,
∴点B的坐标为(![]() ,0);
,0);
(2)∵点A(2,3),B(![]() ,0),
,0),
∴AB=![]() ,
,
∵四边形ABCD是菱形,
∴AD=AB=![]() ,AD∥BC,
,AD∥BC,
∵点C在x轴正半轴上,点D在第一象限,
∴D(2+![]() ,3);
,3);
(3)存在,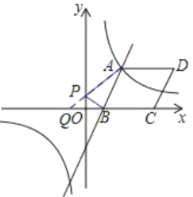
如图,作点B(![]() ,0)关于y轴的对称点Q的坐标为(
,0)关于y轴的对称点Q的坐标为(![]() ,0),连接AQ交y轴于点P,此时PA+PB的值最小,
,0),连接AQ交y轴于点P,此时PA+PB的值最小,
设直线AQ的解析式为:y=mx+b,
则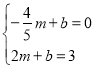 ,解得:
,解得: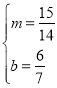 ,
,
∴直线AQ的关系式为![]() ,
,
当x=0时,y=![]()
∴直线AQ与y轴的交点为P(0,![]() ).
).

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目